Planung und Ausführung von Tunnelbauwerken im klüftigen Fels nach der AJRM-Methode – Teil 2
Credit/Quelle: [6]
Credit/Quelle: Interfels GmbH
Credit/Quelle: [5, 6, 10]
Credit/Quelle: [6, 7]
Credit/Quelle: [6, 16]
Credit/Quelle: [5, 6, 17]
Credit/Quelle: [5, 6]
Credit/Quelle: [5, 6]
Credit/Quelle: [6]
Credit/Quelle: [23]
Credit/Quelle: [6, 16]
Credit/Quelle: [6, 16]
Credit/Quelle: [6, 16]
Credit/Quelle: [5, 6]
Der erste Teil dieses Artikels wurde in tunnel 3/2021 [15] veröffentlicht. Dort wird die AJRM Methode vorgestellt und das zugrunde liegende felsmechanische Modell erläutert. Anhand von Fallstudien verdeutlichen die Autoren die Vorteile einer wirklichkeitsnahen Erfassung des Verhaltens von klüftigem Fels sowie des Zusammenwirkens von Baugrund und Bauwerk. Wie angekündigt, befasst sich der vorliegende Teil 2 des Artikels mit dem felshydraulischen Modell und zugehörigen Fallbeispielen sowie mit der Bestimmung der erforderlichen Kennwerte. Damit liegt eine gesamthafte Methode für einen sicheren und wirtschaftlichen Entwurf von Bauwerken sowie für die Grundwassermodellierung im klüftigen Fels vor.
4 Bestimmung der felsmechanischen Kennwerte
4.1 Labor- und Feldversuche
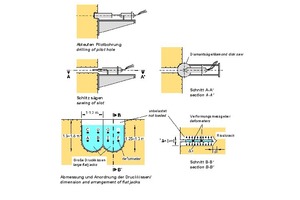
Die Trennflächen haben sowohl auf die Verformbarkeit als auch auf die Festigkeit eines Felses einen entscheidenden Einfluss. Um zuverlässige Angaben zur Verformbarkeit des Felses zu erhalten, muss man deshalb streng genommen Felsvolumina testen, deren Größe ein Mehrfaches des Trennflächenabstands beträgt. Da sich Proben mit derartigen Abmessungen kaum gewinnen und in ein Labor transportieren lassen, wurden schon in den Anfängen der Felsmechanik Feldversuche entwickelt, mit denen sich große Volumina untersuchen lassen. Beim Large Flat Jack Test beispielsweise werden Druckkissen mit der Größe von einem bis mehreren Quadratmetern in gesägte Schlitze eingeführt, und es werden die Schlitzöffnungen in Abhängigkeit von der aufgebrachten Druckspannung gemessen (Bild 16 [5, 6]).
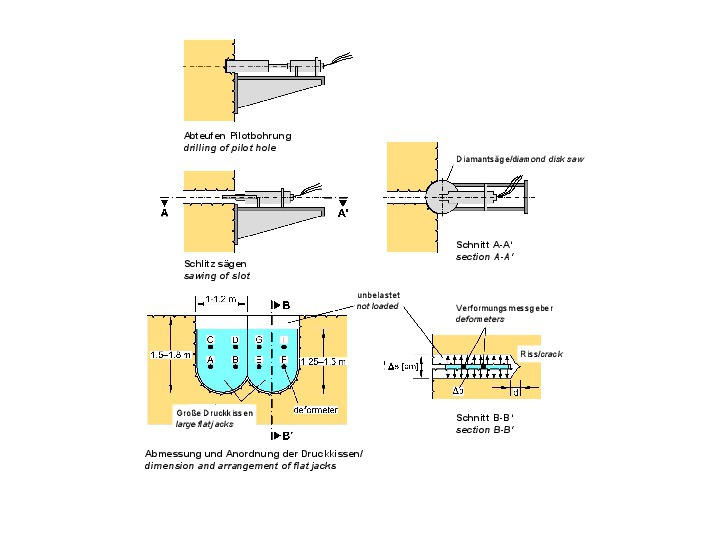16 | Druckkissenversuch Credit/Quelle: [6]
Aus diesen Messergebnissen kann man dann auf den Verformungsmodul des Felses schließen. Aus Kostengründen werden diese Versuche nicht so oft durchgeführt. Vielmehr werden im Zuge von Erkundungsbohrungen häufig Bohrlochaufweitungsversuche wie Dilatometer- oder Pressiometerversuche durchgeführt. Bei diesen Versuchen sind die Abmessungen des getesteten Volumens klein, weshalb der Einfluss der Trennflächen auf die Verformbarkeit meist nicht repräsentativ erfasst wird, In der Folge liefern diese Versuche in der Regel zu große Moduln. Dies muss bei der Aus- und Bewertung der Versuchsergebnisse und der Ableitung der Kennwerte entsprechend berücksichtigt werden.
Die Festigkeit der Trennflächen lässt sich zuverlässig auch nur mit großmaßstäblichen Versuchen bestimmen. Hierfür kommen direkte Scherversuche in Betracht (Bild 17 [5, 6]). Die Festigkeit des unzerklüfteten Gesteins lässt sich dagegen in Laborversuchen an Bohrkernen bestimmen.
17 | Großscherversuch Credit/Quelle: Interfels GmbH
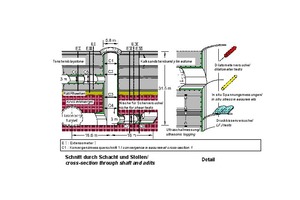
Bei großen Bauvorhaben des Verkehrstunnelbaus oder des Wasserbaus empfiehlt es sich, felsmechanische Untersuchungsprogramme in Verbindung mit vorgezogenen Baumaßnahmen wie Zugangsstollen, Lüftungsschächten o. ä. durchzuführen. Bild 18 [5, 6, 10] zeigt ein einschlägiges Beispiel, bei dem ein Lüftungsschacht und zwei Erkundungsstollen vor Beginn der Haupt-Baumaßnahme aufgefahren wurden.
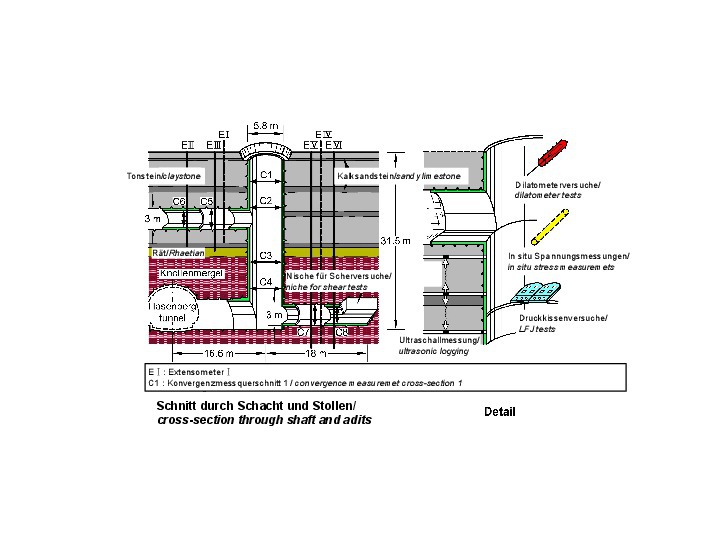18 | Felsmechanisches Untersuchungsprogramm Credit/Quelle: [5, 6, 10]
Hier wurden Druckkissenversuche (LFJ-Tests), Großscherversuche, Dilatometerversuche, Ultraschallmessungen und Primärspannungsmessungen durchgeführt. Außerdem wurden die ausbruchbedingten Verschiebungen mit Hilfe von Extensometern und Konvergenzmessgeräten gemessen. Auf der Grundlage der Ergebnisse der felsmechanischen Versuche und einer Interpretation der gemessenen Verschiebungen mit Hilfe numerischer Berechnungen gelang es, ein zuverlässiges felsmechanisches Modell mit den benötigten Kennwerten zu erarbeiten.
Die mit den Untersuchungen verbundenen Investitionen lassen sich, wie erwähnt, mit vorgezogenen Baumaßnahmen verbinden. Sie zahlen sich durch die Möglichkeiten einer sicheren und wirtschaftlichen Planung und Bauausführung auf der Grundlage abgesicherter und realistischer Kennwerte in der Regel um ein Vielfaches aus.
Bei Vorliegen einschlägiger Erfahrungen der beteiligten Fachleute ist es allerdings auch möglich, die erforderlichen Kennwerte anhand kleinmaßstäblicher Versuche zu ermitteln (vgl. Kap. 4.2 und 4.3).
4.2 Interpretation der Ergebnisse von Messungen bei der Baudurchführung
Im modernen Tunnelbau beinhalten die Standsicherheitsnachweise außer der Bemessung der temporären Sicherung und der Auskleidung auch Prognosen der zu erwartenden Verschiebungen. Weiterhin werden während des Vortriebs die Verschiebungen der Hohlraumwand und des umgebenden Gebirges fortlaufend gemessen und mit den o. g. Prognosen verglichen. Auf dieser Grundlage werden die Vortriebsarbeiten und dabei insbesondere die Sicherungsmittel an die Gegebenheiten angepasst.
Aus der Interpretation (Kalibrierung) der Messergebnisse mit geeigneten felsmechanischen Modellen und Berechnungsverfahren lassen sich aber auch zuverlässige felsmechanische Kennwerte ableiten. Damit lassen sich etwaige Defizite aus vorherigen Erkundungsphasen (vgl. Kap. 4.1) ausgleichen, wenn die sonstigen Randbedingungen (z. B. vertragliche) eine flexible Anpassung an die Gegebenheiten zulassen. Auch auf diesem Weg der Nachrechnung haben die Autoren Erfahrungen in zahlreichen unterschiedlichen Gebirgsverhältnissen gesammelt und einen umfangreichen Erfahrungsschatz aufgebaut.
4.3 Erfahrungswerte
Aus dem oben erwähnten Erfahrungsschatz werden nachstehend einzelne Beispiele aufgeführt.
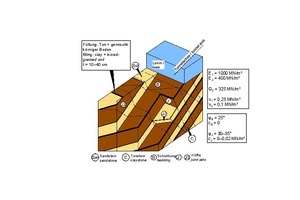
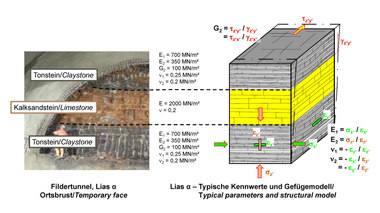
Im Zuge der Planung und des Baus eines Straßentunnels in Wuppertal [7] wurde das in Bild 19 dargestellte felsmechanische Modell erarbeitet.
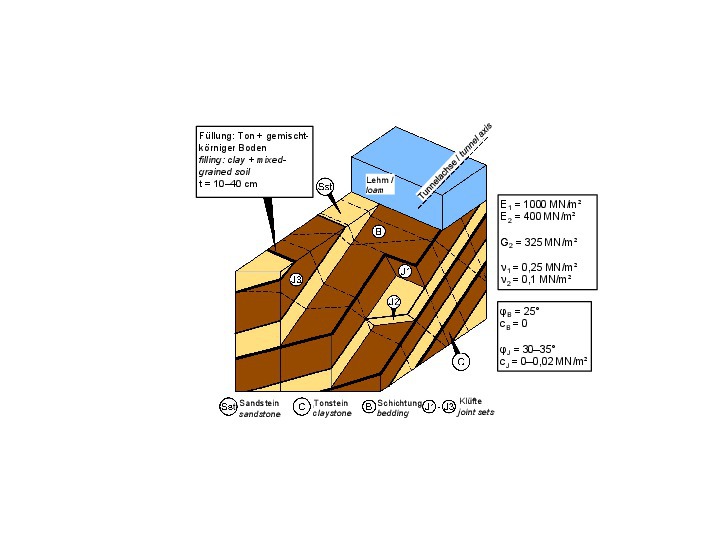19 | Sedimentgestein (Devon) mit Tonfüllungen der Schichtfugen Credit/Quelle: [6, 7]
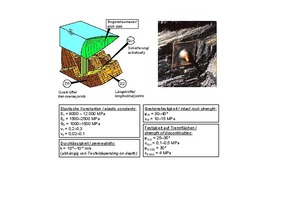
Es zeigt unterhalb einer Lockergesteinsdecke aus bindigem Boden eine Wechsellagerung aus Sand- und Tonsteinen. Die Schichtfugenfüllungen aus Ton und gemischtkörnigem Boden führen zu einer Anisotropie der Verformbarkeit, die sich mit den dargestellten fünf elastischen Konstanten beschreiben lässt (Bild 19, vgl. auch Bild 2 im Teil 1 der Veröffentlichung [15]). Die Scherfestigkeit parallel zur Schichtung lässt sich durch einen Reibungswinkel von φB = 25° und eine Kohäsion von cB = 0 kN/m² beschreiben. Für die Klüfte kann in der Regel außer dem Reibungswinkel noch eine Kohäsion in Ansatz gebracht werden (Bild 19).
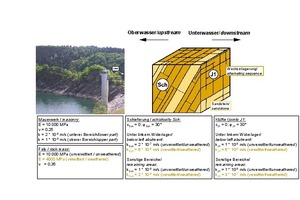
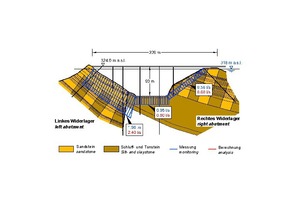
Für die Wechsellagerung aus Sand- und Tonstein, wie sie im Bereich der Urfttalsperre in der Eifel angetroffen wurde, konnte ein isotropes Spannungsdehnungsverhalten im elastischen Bereich festgestellt werden. Allerdings musste hier zwischen einem oberflächennahen, verwitterten Bereich und dem tieferen, unverwitterten Bereich unterschieden werden (Bild 20, [6, 16]). Die Scherparameter der Schieferung und der Klüftung sind ebenfalls in Bild 20 zusammengestellt. Weiterhin finden sich dort die Durchlässigkeitsbeiwerte parallel zur Schieferung und Klüftung der Formation. Dabei ist festzuhalten, dass die Wasserdurchlässigkeit des linken Felswiderlagers größer ist als die in den anderen Bereichen (vgl. Kapitel 5 und 6).
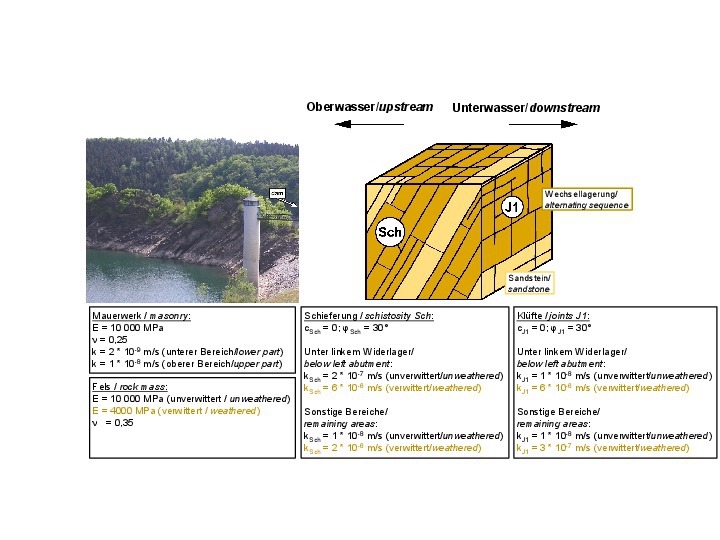20 | Felsmechanisches Modell für die Gründung der Urftstaumauer Credit/Quelle: [6, 16]
Das felsmechanische Modell eines Tonschiefers aus dem Ernstbachtal in der Nähe der Stadt Rüdesheim am Rhein zeigt das Bild 21 [17, 6, 5]. Man erkennt, dass der Tonschiefer sowohl hinsichtlich der Verformbarkeit als auch hinsichtlich der Festigkeit stark anisotrop ist. Das ist im Wesentlichen durch die Schieferung bedingt.
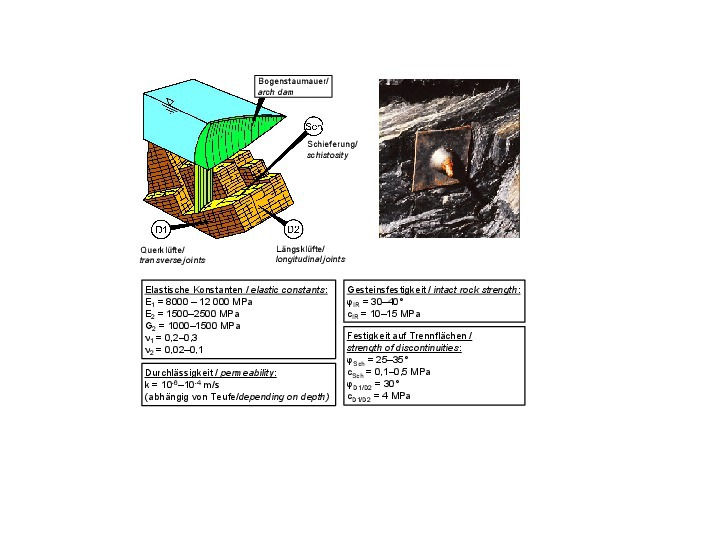21 | Felsmechanisches Modell für einen Tonschiefer Credit/Quelle: [5, 6, 17]
Weitere Beispiele dieser Art finden sich in [6]. Die dort für verschiedene Gebirgsverhältnisse genannten Kennwerte können für erste Betrachtungen in frühen Projektphasen, wenn noch keine anderen Ergebnisse vorliegen, zugrunde gelegt werden, wenn die Projektbeteiligten über entsprechende Erfahrungen verfügen.
5 Felshydraulisches Modell
Das unzerklüftete Gestein besitzt erfahrungsgemäß eine sehr geringe Wasserdurchlässigkeit und kann – von wenigen Ausnahmen abgesehen – als undurchlässig angenommen werden. Die Sickerströmung im Fels erfolgt in der Regel durch die Trennflächen (vgl. Bild 22, links unten) und ist zumeist laminar.
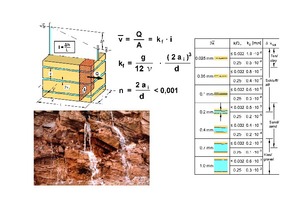
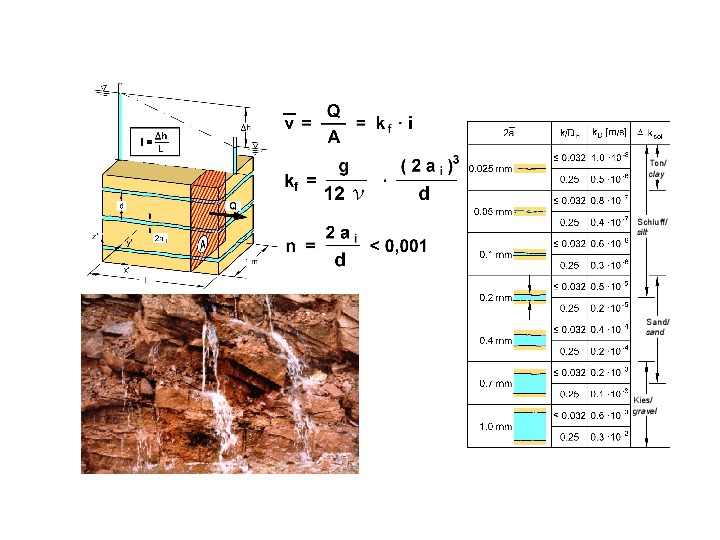22 | Sickerströmung in Trennflächenscharen und Wasserdurchlässigkeit in Abhängigkeit von der Öffnungsweite der Trennflächen Credit/Quelle: [5, 6]
Die mittlere Fließgeschwindigkeit für die eindimensionale Strömung in einer Trennfläche lässt sich durch die Integration der Navier-Stoke‘schen Differentialgleichungen herleiten. Für die eindimensionale Sickerströmung durch eine Schar paralleler Trennflächen mit konstantem Abstand und konstanter Öffnungsweite definiert man in Anlehnung an das Gesetz von Darcy aus der Bodenmechanik eine auf den Gesamtquerschnitt bezogene Filtergeschwindigkeit (vgl. [5, 6, 10] und Bild 22 links oben). Diese Filtergeschwindigkeit ist proportional zur 3. Potenz der Spaltweite 2ai und umgekehrt proportional zum Trennflächenabstand s¯. Damit ist die Öffnungsweite der Trennflächen 2ai neben dem Trennflächenabstand und der Viskosität des Wassers ein wesentlicher Einflussfaktor für die Strömung im Fels.
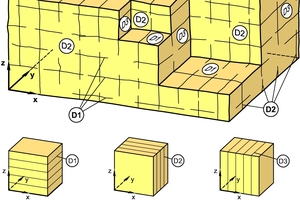
Für den räumlichen Fall eines Felses mit drei senkrecht aufeinander stehenden Trennflächenscharen lässt sich durch Superposition der Durchlässigkeiten der einzelnen Trennflächenscharen eine Durchlässigkeitsmatrix ermitteln, die nur in der Hauptdiagonale besetzt ist und die multipliziert mit den drei Komponenten des räumlichen Gefälles die drei Komponenten der Filtergeschwindigkeit ergibt (Bild 23 [5, 6]):
{v} = [K] ∙ {I}
Bei dieser Vorgehensweise werden die Strömungsverluste entlang der Schnittlinien der Trennflächen vernachlässigt. Diese Annahme ist bei den geringen in der Praxis auftretenden Fließgeschwindigkeiten zulässig. Entsprechend wird im Falle von Trennflächenscharen vorgegangen, die nicht senkrecht aufeinander stehen [5, 6].
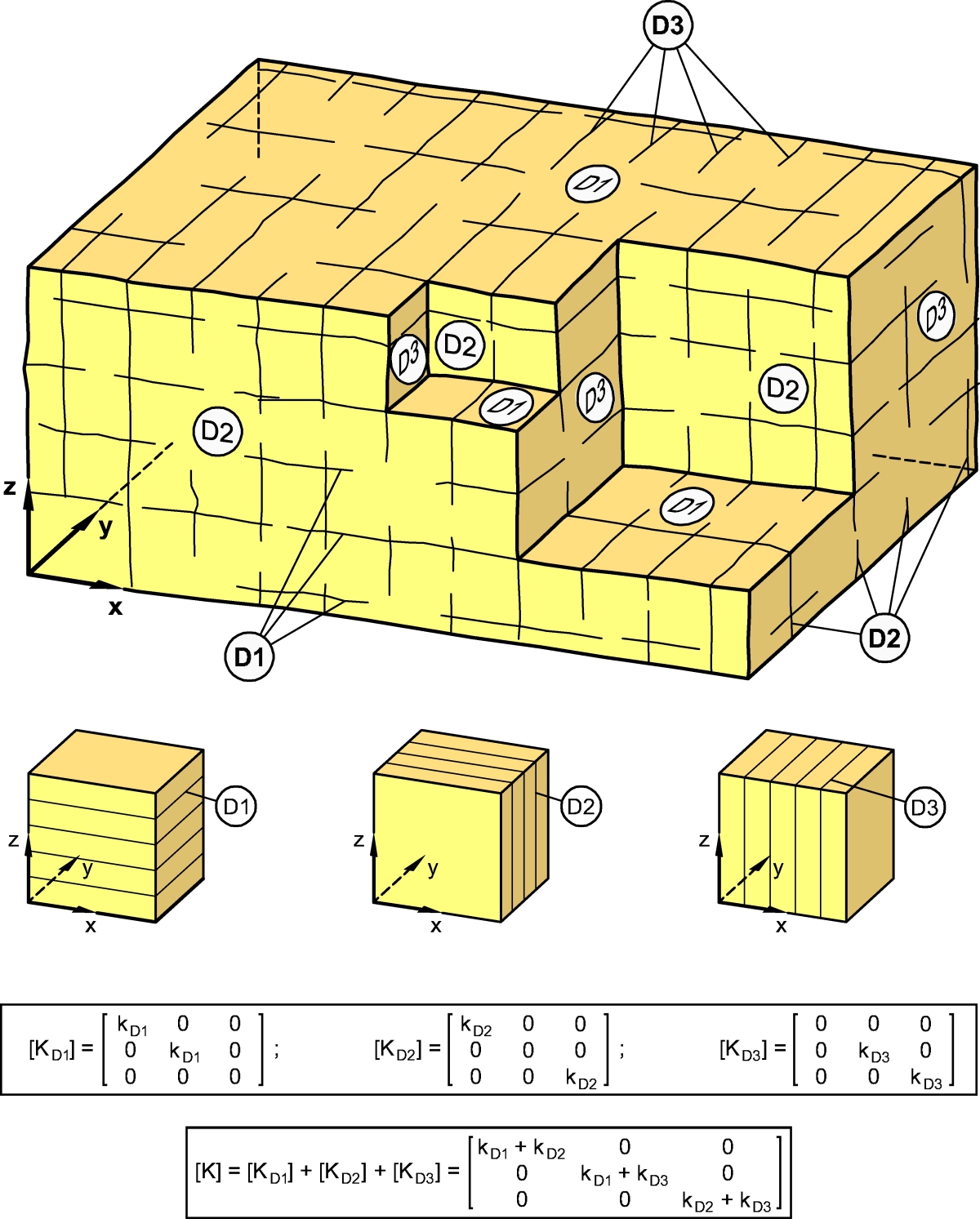23 | Wasserdurchlässigkeit eines Felses mit drei senkrecht aufeinander stehenden Trennflächenscharen Credit/Quelle: [5, 6]
In den meisten Fällen ist die Wasserdurchlässigkeit des Felses stark anisotrop. Lediglich in dem Sonderfall dreier senkrecht aufeinander stehenden Trennflächen mit gleicher Durchlässigkeit besitzt ein Fels eine isotrope Durchlässigkeit. Die Anisotropie wirkt sich stark auf die Richtung der resultierenden Geschwindigkeit der Sickerströmung und des Strömungsdrucks aus. Dadurch unterscheidet sich die Untersuchung der Sickerströmung vom Fels deutlich von entsprechenden Betrachtungen in grobkörnigen Böden.
Bild 22, rechts, enthält eine Zusammenstellung der Durchlässigkeitsbeiwerte eines Felses mit einer Trennflächenschar mit einem konstanten Abstand von 1 m und konstanter Spaltweite. Man erkennt, dass die Wasserdurchlässigkeit eines Felses bei vergleichsweise geringen Öffnungsweiten der Trennflächen von 0,7–1,0 mm bereits die Werte eines Kiessandes annimmt. Andererseits sind die Kluftvolumina und damit auch das Speichervermögen des Felses deutlich geringer als die eines Kieses. Beide Aspekte sind sehr wesentlich und bei Planungsaufgaben zu beachten. So kann beispielsweise ein Anschneiden von wassererfüllten Trennflächen geringer Spaltweite beim Bau zu erheblichen Wasserzuflüssen führen. Auch führt das geringe Kluftvolumen dazu, dass der Grundwasserspiegel nach Niederschlägen wesentlich stärker ansteigt als z. B. in grobkörnigen Lockergesteinen. Außerdem ist das geringe Kluftvolumen bei Wassergewinnungsanlagen zu berücksichtigen.
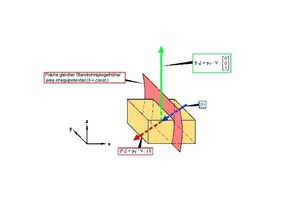
Die von der Sickerströmung auf den Fels übertragenen Volumenkräfte teilen sich wie in der Bodenmechanik in den hydrostatischen Auftrieb {Fu} und den senkrecht zu den Flächen gleicher Standrohrspiegelhöhen wirkenden, hydrodynamischen Strömungsdruck {Fs} auf (Bild 24 [6]).
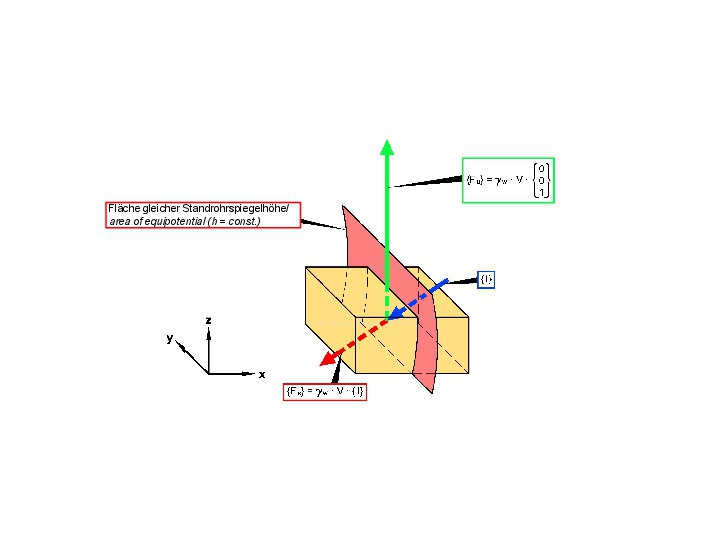24 | Auftrieb und Strömungsdruck im klüftigen Fels Credit/Quelle: [6]
Der Strömungsdruck kann erheblichen Einfluss auf die Standsicherheit beispielsweise von Böschungen und Staumauerwiderlagern sowie auch der Ortsbrust im Tunnelbau haben. Die Sickerströmung muss deshalb in Standsicherheitsnachweisen berücksichtigt werden. Wie bereits erwähnt, ist allerdings auch hier zu bedenken, dass die Wasserdurchlässigkeit des Felses anisotrop ist und sich die Potentialverteilung nicht in der gleichen einfachen Weise einstellt und ermitteln lässt, wie bei bodenmechanischen Fragestellungen in grobkörnigen Böden. Das ist bei Standsicherheitsnachweisen entsprechend zu berücksichtigen.
6 Fallbeispiel
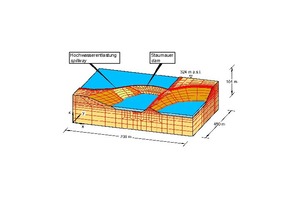
Die ca. 60 m hohe Urfttalsperre wurde ungefähr vor 120 Jahren als Schwergewichtsmauer geplant und aus Bruchsteinmauerwerk gebaut. Sie liegt in der Eifel in der Nähe der Stadt Aachen (Bild 25 [16]). Nach heutigen Kriterien [18] ließ sich die Standsicherheit der Staumauer nicht mehr für alle Lastfälle nachweisen.
25 | Urfttalsperre Credit/Quelle: [23]
Das aus diesem Grunde erforderliche Sanierungskonzept sah den Bau von zwei Dränage- und Inspektionsstollen sowie die Anordnung vertikaler Dränagebohrungen in der Staumauer vor [6]. Außerdem wurde im Standsicherheitsnachweis die Gewölbewirkung der doppelt gekrümmten Mauer in Anspruch genommen und somit berücksichtigt, dass ein Teil des auf die Oberwasserseite der Mauer wirkenden Wasserdrucks in die Felswiderlager eingeleitet wird. Diese Annahme führt dazu, dass in Höhe der Gründung auf der Oberwasserseite keine Zugspannungen mehr auftreten [16]. Die Genehmigungsbehörde stimmte dieser Lösung mit der Auflage zu, dass das in den 3D-FE-Berechnungen nachgewiesene Tragverhalten mittels nach der Sanierung am Bauwerk durchgeführter Messungen bestätigt wird. Dazu gehörte auch die Untersuchung der Um- und Unterläufigkeit der auf Tonschiefer gegründeten Mauer.
Das aus den Ergebnissen der Voruntersuchungen und der nach der Sanierung durchgeführten Kalibrierung resultierende felsmechanische Modell und die charakteristischen Kennwerte sind in Bild 20 zusammengestellt. Die für die Sickerströmung maßgebenden Trennflächen sind die vertikale, vom Ober- zum Unterwasser streichende Kluftschar J1 und die senkrecht zum Tal streichende, steil zum Oberwasser einfallende Schieferung Sch. Für beide Trennflächenscharen ist zwischen einer oberflächennahen, verwitterten Zone und einem darunterliegenden unverwitterten Bereich zu unterscheiden. Die Durchlässigkeitsbeiwerte liegen in der Größenordnung von 10-6–10-8 m/s. Die Schieferung weist dabei eine größere Durchlässigkeit auf als die Klüftung, bzw. zum Teil sind die Durchlässigkeiten auch gleich.
In Anbetracht der geringen Durchlässigkeiten wurde ein Injektionsschleier als nicht erforderlich angesehen. Auch ein Dränagefächer im Fels war nicht erforderlich, weil die zum Oberwasser einfallende Schieferung aufgrund ihrer Durchlässigkeit wie eine Dränage wirkte.
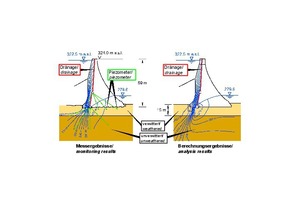
Aus der 3D-FE-Berechnung zur Um- und Unterläufigkeit der Mauer (Bild 26) ergaben sich die in Bild 27 dargestellten Potentialverteilungen, die durch die Ergebnisse der im Untergrund und der Mauer durchgeführten piezometrischen Messungen bestätigt wurden.
Auch die im unteren Kontrollgang anfallenden Sickerwassermengen stimmen mit den Rechenergebnissen gut überein (Bild 28).
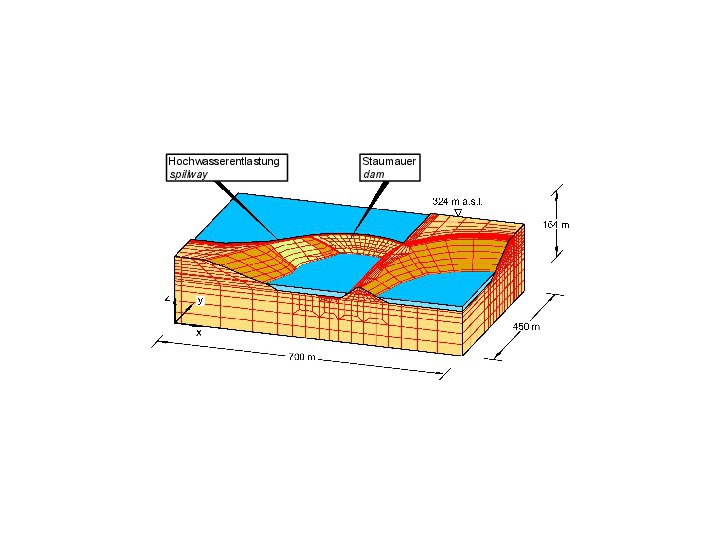26 | FE-Netz zur Untersuchung der Sickerströmung durch Mauer und Untergrund Credit/Quelle: [6, 16]
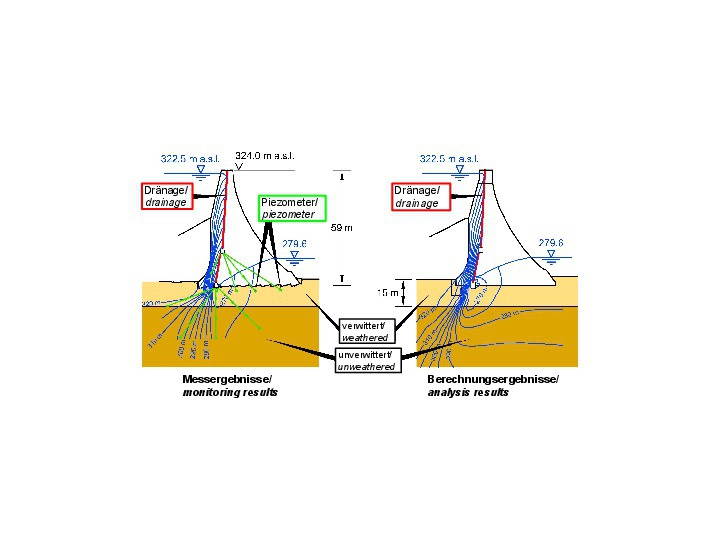27 | Sickerströmung durch Mauer und Untergrund, Vergleich Rechnung und Messung Credit/Quelle: [6, 16]
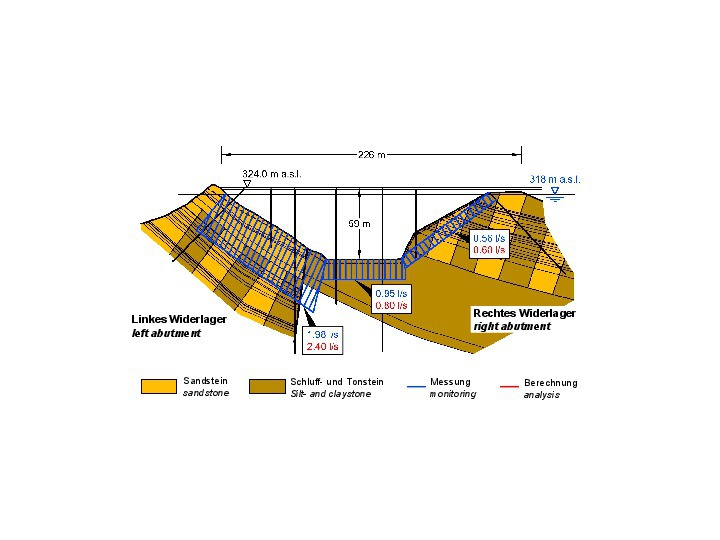28 | Sickerwasserverluste, Vergleich Rechnung und Messung Credit/Quelle: [6, 16]
7 Bestimmung der felshydraulischen Kennwerte
Die für die Anwendung des beschriebenen felshydraulischen Modells erforderlichen Kennwerte lassen sich mit den allgemein üblichen Untersuchungsmethoden bestimmen. Deshalb werden diese nachstehend nur kurz angerissen.
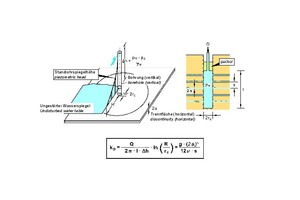
Beim Lugeon-Versuch wird in einem nach oben durch einen Packer abgesperrten Bohrlochabschnitt unter Druck Wasser in den umgebenden Fels gepresst. Aus der aufgenommenen Wassermenge und dem aufgebrachten Druck wird dann der Durchlässigkeitsbeiwert des Felses ermittelt (Bild 29 [6]). Um die Durchlässigkeit der anstehenden Trennflächenscharen zu ermitteln und damit die Komponenten der Durchlässigkeitsmatrix bestimmen zu können, empfiehlt es sich, die Bohrlöcher zumindest annähernd senkrecht zu den jeweiligen Trennflächenscharen auszurichten.
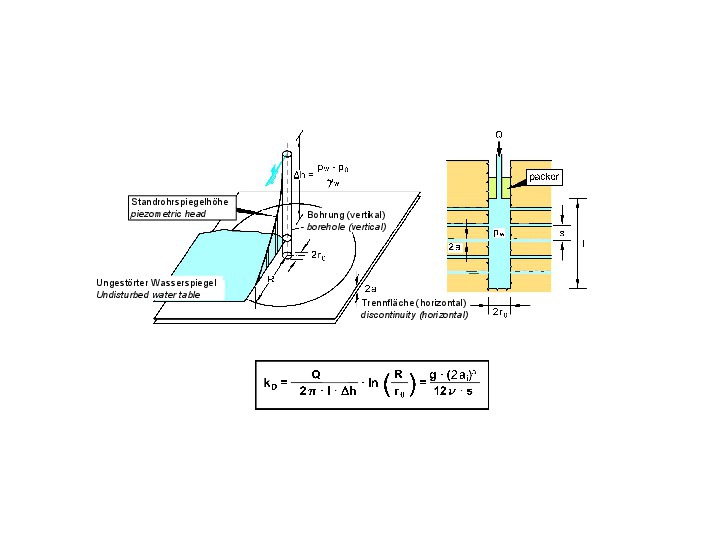29 | Auswertung eines Lugeon-Versuchs
Credit/Quelle: [5, 6]
Schluckversuche in Bohrlöchern mit konstanter oder fallender Druckhöhe eignen sich ebenfalls zur Bestimmung der Wasserdurchlässigkeit eines Felses [19, 6].
Während sich bei den vorstehend genannten Versuchen der untersuchte Bereich auf die unmittelbare Umgebung des jeweiligen Bohrlochs beschränkt, lassen sich mit Pumpversuchen, wenn diese durch Piezometermessungen in der Umgebung des beaufschlagten Bohrlochs ergänzt werden, Durchlässigkeiten für größere Felsbereiche ermitteln [20]. Für Fels mit geringen Durchlässigkeitsbeiwerten eignen sich Pulstests und auch Luftdurchlässigkeitsversuche [6, 21].
Eine Versuchseinrichtung, mit der unter Verwendung von Acrylatgel oder auch Wasser als Versuchsmedium Durchlässigkeitsbeiwerte bis zu 10-10 m/s gemessen werden können, wurde von der WBI GmbH entwickelt und eingesetzt [22].
8 Zusammenfassung und Schlussfolgerungen
Eine sichere und wirtschaftliche Planung von Bauwerken in klüftigem Fels setzt eine realitätsnahe Berücksichtigung des Zusammenwirkens von Baugrund und Bauwerk voraus. Das Bettungsmodulverfahren sowie Klassifizierungsmethoden (Q, RMR, RMi) erfüllen diese Voraussetzung nicht. Auch das von Hoek-Brown eingeführte Verfahren auf der Basis des GSI und des Hoek-Brown Bruchkriteriums erfüllt die Anforderungen in vielen Fällen nicht, da es von isotropem Verhalten des Felses ausgeht.
In dem vorliegenden zweiteiligen Beitrag (Teil 1 in [15]) wird dagegen ein Modell für den anisotropen, geklüfteten Fels vorgestellt, das von den Autoren bereits seit vielen Jahren in der Planung und beim Bau von Felsbauwerken mit großem Erfolg angewendet wird. Mit einer realitätsnahen Beschreibung des mechanischen und hydraulischen Verhaltens von klüftigem Fels unter Berücksichtigung der Anisotropie gelingt es, sichere und wirtschaftliche Lösungen zu finden.
In dem zweiteiligen Beitrag werden sowohl das mechanische als auch das hydraulische Modell erläutert. Es wird auf die Bestimmung der erforderlichen Kennwerte eingegangen, und es werden einige Fallbeispiele dargestellt. In der Gesamtheit werden damit die Grundlagen und Anwendungsbeispiele einerseits für die statische Betrachtung, Bemessung und Planung von Bauwerken im Fels und andererseits für hydrogeologische Betrachtungen (Grundwassermodelle) erläutert, wobei die aus der Sickerströmung resultierenden Kräfte selbstverständlich auch im statischen Nachweis zu berücksichtigen sind.
Die Autoren möchten ausdrücklich zur fachlichen Diskussion einladen und hoffen, dass auch in der Forschung weiter an der Verfeinerung der AJRM-Methode gearbeitet wird. Schon jetzt würde eine breite Anwendung der vorgestellten Vorgehensweise zu kostengünstigeren und sichereren Lösungen führen, als sie mit den herkömmlichen Methoden der Planung möglich sind.
References/Literatur
[1] Abbas, S.M.; Konietzky, H.: Rock mass classification systems. Chapter 10 of E-Book “Introduction into geomechanics”. Download from “https://tu-freiberg.de/fakultaet3/gt/felsmechanik/forschung-lehre/e-book” on April 26, 2021, 11.15h.
[2] Sommer, R.: Kritische Wertung der Methoden der Gebirgsklassifizierung im Tunnelbau. Geotechnik in Forschung und Praxis,
WBI-PRINT 16, VGE: Essen, 2009.
WBI-PRINT 16, VGE: Essen, 2009.
[3] Wittke W., Sommer, R.: Designs in jointed rock. World Tunneling July/August 2011, pp. 30 to 34.
Corresponding discussion:
+ Barton, N.: A measured response. World Tunneling September 2011, pp. 13 to 17.
+ Wittke, W.; Sommer, R.: Answer to the “measured response”. World Tunneling, 6.10.2011.
[4] Hoek, E.; Carranza-Torres, C.; Corkum, B.: Hoek-Brown Failure Criterion – 2002 Edition. In: Hammah, R.; Bawden, W.; Curran, J. and Telesnicki, M., eds., Mining and Tunneling Innovation and Opportunity.
[5] Wittke, W.: Felsmechanik, Grundlagen für wirtschaftliches Bauen im Fels. Springer-Verlag, Berlin 1984. ISBN-Nr.: 3-540-13016-0 / 0-387-13016-0.
English Version:
Wittke, W.: Rock mechanics – Theory and application with case histories. Springer: Berlin, Heidelberg, New York, Tokyo, 1990. ISBN-Nr.: 3-540-52719-2 / 0-387-52719-2
[6] Wittke, W.: Rock Mechanics based on an Anisotropic Jointed Rock Model (AJRM), Verlag Ernst & Sohn GmbH & Co. KG, Berlin 2014. ISBN-Nr.: 978-3-433-03079-0.
[7] Wittke, W.; Pierau, B.; Erichsen, C.: Statik und Konstruktion der Spritzbetonbauweise. Geotechnik in Forschung und Praxis, WBI-Print 5, Verlag Glückauf GmbH, Essen, 2002. ISBN-Nr.: 3-7739-1305-2.
English version:
New Austrian Tunneling Method (NATM) – Stability Analyses and Design. Available for download in WBI-Library on
www.wbionline.de.
www.wbionline.de.
[8] Wittke, W.; Wittke, M. Druffel, R., Rath, A.; Osthoff, G.: Großquerschnitte im Anfahrbereich Hauptbahnhof Süd, Statische Berechnungen, Senkungsprognosen und Baubetriebliche Aspekte. Vortrag anlässlich des 5. Felsmechanik- und Tunnelbautages im WBI-Center am 23.05.2019. WBI-Print 22, Weinheim, 2019. ISBN-Nr.: 978-3-00-063255-6.
[9] https://mobil.hessen.de/a44 mobil.hessen.de: A44 Kassel – Herleshausen (abgerufen am 22.10.2019, 13.22 Uhr).
[10] Wittke, W.; Wittke-Schmitt, B.; Wittke-Gattermann, P.: Das Modell AJRM als Grundlage für wirtschaftliches und sicheres Planen und Bauen im klüftigen Fels. Vortrag anlässlich des 5. Felsmechanik- und Tunnelbautages im WBI-Center am 23.05.2019. WBI-Print 22, Weinheim, 2019. ISBN-Nr.: 978-3-00-063255-6
[11] Green Line in Katar: Baugrube Station Education City South East. Projektunterlagen von anderen Projektbeteiligten (Planer), 2014. Unveröffentlicht.
[12] www.rocscience.com/documents/pdfs/uploads/8079.pdf: RocLab 1.0 Rock Mass strength analysis using the generalized Hoek-Brown failure criterion. (Abgerufen am 27.04.2021, 11.25 Uhr)
[13] Wittke-Schmitt, B.; Küpper, H.-J.; Wenkenbach, H.: Green Line in Qatar, bergmännische Unterfahrung einer 8spurigen Straße in Doha. Vortrag anlässlich des 3. Felsmechanik- und Tunnelbau-Tags im WBI-Center am 11.05.2017. WBI-PRINT 20, Weinheim, 2017.
ISBN-NR.: 978-3-00-057227-2
ISBN-NR.: 978-3-00-057227-2
[14] Wenkenbach, H.; Wittke, M.; Wittke-Schmitt, B.; Küpper, H.-J.: Green Line Katar: Konventionelle Tunnelvortriebe, Planung und Ausführung auf der Grundlage der AJRM-Methode. Veröffentlichung in der Zeitschrift „Tunnel“, Jahrgang 37, 05/2018, S. 16 bis 26, Bauverlag BV GmbH, Gütersloh.
[15] Wittke, M.; Wittke-Schmitt, B.; Wittke-Gattermann, P.; Wittke, W.: Sichere und wirtschaftliche Planung und Ausführung von Tunnelbauwerken im klüftigen Fels nach der AJRM-Methode – Teil 1. In Zeitschrift Tunnel 3/2021. Bauverlag BV GmbH, Gütersloh, 2021.
[16] Wittke, W.; Wittke, M.; Kiehl, J. R.: Interaction of a masonry dam and the rock foundation. Geotechnical and Geological Engineering 30, Special Issue on Selected Topics in Rock Mech. and Rock Eng., 581–601, 2012.
[17] Wittke, W.; Schetelig, K.: Gründung einer Bogengewichtsmauer in Schiefer. In: Proc. Baugrundtagung, Berlin, 1978.
[18] DIN 19700-11 (German standard): Stauanlagen - Teil 11: Talsperren (Dam plants – Part 11: Dams). Beuth: Berlin, 2004.
[19] Schreiner, M.; Kreysing, K.: Geotechnik Hydrologie S. 495–508. Springer 1998.
[20] Wittke-Gattermann, P.; Druffel, R.: Vortrieb eines Autobahntunnels unter einem Flußtal. Taschenbuch für den Tunnelbau 2015,
Verlag Ernst & Sohn GmbH & Co. KG, Berlin 2015
Verlag Ernst & Sohn GmbH & Co. KG, Berlin 2015
[21] Wittke, B: Permeabilität von Steinsalz, Theorie und Experiment. WBI-PRINT 3, Verlag Glückauf, Essen, 1999. ISBN: 3-7739-1303-6.
[22] Wittke, M.; Schmitt, D.; Osthoff, G.: Einpressungen von Acrylatgel und Polyurethan zur Abdichtung des anhydritführenden Gipskeupers im Bereich der Tunnel nach Ober- und Untertürkheim. Vortrag anlässlich des 5. Felsmechanik- und Tunnelbautages im WBI Center am 23.05.2019. WBI-PRINT 22. Weinheim, 2019. ISBN: 978-3-00-063255-6.
[23] Polcyk, H.: Mehrjährige Beobachtungen des Verhaltens der Urfttalsperre. In: 20 Jahre WBI, Vorträge des Seminars aus Anlass des 20-jährigen Bestehens der WBI GmbH. Geotechnik in Forschung und Praxis. WBI-PRINT 10, Glückauf: Essen, 2001.
