Tunnelplanung – Felsmechanische Modelle (AJRM) vs. Klassifizierung
Der vorliegende Artikel beleuchtet zwei Ansätze zur Vorgehensweise bei der Planung im Tunnelbau: das AJRM (Anisotropic Jointed Rock Model) und auf Gebirgskennziffern basierende Klassifizierungssysteme. Das AJRM berücksichtigt die Anisotropie des Gebirges und wird u.a. im Tunnelbau erfolgreich genutzt. Demgegenüber stehen Klassifizierungssysteme wie das Q-System, RMR und RMi, die vor allem in Skandinavien und im angelsächsischen Raum Verbreitung finden. Die Anwendung dieser Klassifizierungssysteme in Sedimentgesteinen ist jedoch nach Ansicht der Autoren mit großen Risiken behaftet und bietet keine ausreichende Zuverlässigkeit bei komplexen geologischen Verhältnissen. Die Autoren schlagen vor, anstelle dieser Systeme verstärkt das AJRM-Modell weiterzuentwickeln.
Credit/Quelle: Ingenieurgemeinschaft A44, Bauabschnitt 4.2 und 5
Das Fachgebiet der Felsmechanik wurde in den 1950er- und 1960er-Jahren begründet. Die Bedeutung des Fachs zeigte sich bereits damals mit der Gründung der International Society for Rock Mechanics – kurz ISRM – im Jahr 1962. Im §2 der seinerzeitigen Satzung wurden die Aufgaben wie folgt definiert:
a) Die wissenschaftliche Erforschung des physikalischen Verhaltens von Fels, insbesondere als inhomogener und anisotroper Körper,
b) Die Entwicklung und Beurteilung der Berechnungsgrundlagen von Bauwerken und Schürfarbeiten im Fels sowie der Gründung von Bauwerken auf Fels,
c) Die mechanische Erklärung tektonischer Phänomene.
In Übereinstimmung mit diesen Zielen wurde in Verbindung mit dem Institut von Prof. Leussink in Karlsruhe, der dem ersten Vorstand der ISRM angehört hat, durch Prof. Wittke und sein Team geforscht. In diesem Zusammenhang hat Prof. Wittke bei Prof. Leussink promoviert und habilitiert. Es wurden Modelle und Berechnungsverfahren erarbeitet, die ab 1974 an der RWTH und ab 1980 bei WBI kontinuierlich weiterentwickelt wurden. Diese, seit 2014 unter dem Begriff AJRM (Anisotropic Jointed Rock Model) zusammengefassten Modellvorstellungen, werden heute sehr erfolgreich u. a. im Tunnelbau angewendet.
Parallel zu diesen Entwicklungen wurde insbesondere im skandinavischen und angelsächsischen Raum eine andere Methode eingeführt – die sogenannten Klassifizierungssysteme bzw. im englischen prescriptive measures. Von Barton et al. wurde 1974 das Q-System eingeführt. Es folgten das RMR- und RMi-System, die durch Bieniawski und Palmström in den Jahren 1974 und 1995 zuerst veröffentlicht wurden.
Im Artikel werden diese Systeme kurz vorgestellt und diskutiert. Es wird gezeigt, dass die Anwendung in Sedimentgesteinen mit großen Risiken behaftet und u. a. auch deshalb nicht zielführend ist. Vielmehr sollte sich die Wissenschaft und Forschung mit der Weiterentwicklung der langjährig erprobten AJRM-Methode befassen. Auch in der Normung sollte der Anwendung der o. g. Klassifizierungssysteme im Tunnelbau weiterhin ein Riegel vorgeschoben werden. Wir hoffen, dass hierauf bei der Überarbeitung des EC 7 entsprechend hingewirkt wurde und wird.
Im Beitrag wird zudem der von Hoek und Brown eingeführte GSI (Geological Strength Index) diskutiert, auf dessen Grundlage zwar Berechnungen möglich sind, für den aber isotrope Verhältnisse angenommen werden, die in den meisten Fällen nicht vorhanden sind.
1 Veranlassung
Mit [1] wurde bereits im Jahr 2009 eine kritische Wertung der Methoden der Gebirgsklassifizierung im Tunnelbau vorgelegt. Diese wurde in den folgenden Jahren in Fachdiskussionen, u. a. in [2], [3] und [4], diskutiert. Erfahrungen, die wir in jüngerer Vergangenheit im Zuge unserer Projektbearbeitung gemacht haben, und die bevorstehende Einführung des neuen EC 7 haben die Autoren dazu veranlasst, das Thema wieder aufzugreifen.
1 | Festgesteine in Deutschland, Übersicht
Credit/Quelle: WBI GmbH
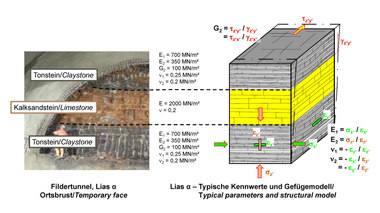
Um das sachgerecht machen zu können, müssen zunächst die geologischen Verhältnisse bzw. die Baugrundverhältnisse betrachtet werden, in denen Tunnel geplant und gebaut werden. Beispielhaft ist auf dem Bild 1 die geologische Übersichtskarte
Deutschlands dargestellt. Man erkennt, dass von der Mitte Deutschlands bis zu den Alpen größtenteils Festgesteine in der Nähe der Geländeoberfläche anstehen. Meist handelt es sich dabei um Sedimentgesteine, die eine ausgeprägte Schichtung und Klüftung aufweisen. Beispielhaft sind im Bild 1 Schichten des Devons (Rittersturz in Koblenz), des Buntsandsteins (A44, Tunnel Alberberg) und des Schwarzjuras (Flughafentunnel Stuttgart) dargestellt. Die Fotos zeigen, dass es bei der Planung von Tunnelbauwerken unabdingbar ist, den Fels, d. h. Gestein und Trennflächen, einschließlich der Anisotropien und Inhomogenitäten wirklichkeitsnah zu erfassen.
2 Planung auf der Grundlage der Felsmechanik
Um die Wissenschaft in dieser Hinsicht weiterzubringen, wurde im Jahr 1962 – entstanden aus dem Salzburger Kreis – die ISRM (International Society for Rock Mechanics and Rock Engineering) gegründet. Die Ziele der Gesellschaft (siehe oben) wurden in der ersten Satzung definiert [6]. Danach ist die Aufgabe der Felsmechanik, den Fels, ähnlich wie den Beton im Massivbau oder den Boden in der Bodenmechanik, berechenbar zu machen.
In Übereinstimmung mit diesen Zielen wurde im Jahr 1969 die Fachsektion Felsmechanik der DGGT gegründet. Im Jahr 1972 fand ein großes Symposium in Deutschland statt, bei dem die Grundlagen der Sickerströmungsberechnungen vorgestellt und diskutiert wurden. Seit dem Jahr 1980 beschäftigt sich die WBI GmbH unter Leitung von Prof. Wittke mit der Anwendung und der Forschung in der Felsmechanik. In diesem Zeitraum sind u. a. [7] und [8] veröffentlicht worden, und seit 2015 wird in diesem Zusammenhang jährlich der Felsmechanik- und Tunnelbautag in Weinheim veranstaltet.
Die angewandte Forschung und Entwicklung der letzten Jahrzehnte ermöglichen es, bei der Planung und Ausführung von Tunnelbauprojekten im Fels entsprechend der allgemein anerkannten Vorgehensweise vorzugehen, nach der auf der Grundlage von geotechnischen Untersuchungen felsmechanische Modelle entwickelt werden. Diese bilden wiederum die Grundlage für die Nachweise der Standsicherheit und der Gebrauchstauglichkeit und schließlich des Entwurfs und der Planung unter Berücksichtigung der einschlägigen Richtlinien und Normen. Nach der Beobachtungsmethode wird das Bauwerksverhalten beim Bau überprüft und mit den Prognosen verglichen. Dieses Vorgehen (AJRM-Methode) wird von der WBI-GmbH inzwischen seit 44 Jahren erfolgreich angewendet.
3 Klassifizierungssysteme
Im angelsächsischen Raum wurde daneben ein etwas anderer Weg verfolgt. Von Hoek-Brown wurde im Jahr 1980 ein Bruchkriterium eingeführt, dass im Jahr 1995 mit dem GSI verknüpft wurde ([9], [10]). Mit den dort eingeführten Methoden sind selbstverständlich Berechnungen möglich, allerdings wird das Tragverhalten des Felses sehr stark vereinfacht und Inhomogenitäten und Anisotropien werden vernachlässigt. Das führt häufig – wie z. B. auch in [17] gezeigt – zu unwirtschaftlichen Bemessungen.
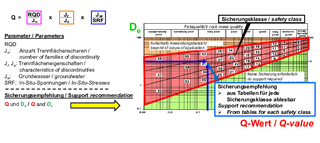2 | Q-System, Ermittlung der Gebirgskennziffern und Ableitung einer Sicherungsempfehlung
Credit/Quelle: WBI GmbH
Aus dem skandinavischen Raum kommend wurden die sogenannten Klassifizierungssysteme eingeführt (Bilder 2 & 8). Im Jahr 1974 wurden das Q-System und das RMR-System und im Jahr 1995 das RMi-System von Palmström erstmalig veröffentlicht [11], [12], [13].
Über diese Gebirgskennziffern soll es möglich sein, über empirische Formeln Kennwerte für den Fels zu ermitteln. Hierauf soll im vorliegenden Beitrag nicht näher eingegangen werden. Es wird jedoch darauf hingewiesen, dass auf dieser Grundlage durchgeführte Berechnungen den gleichen Nachteil haben wie die Methoden nach Hoek-Brown – sie vernachlässigen die Anisotropie und Inhomogenitäten oder treffen hierzu unzulässige, vereinfachende Annahmen. Sie entsprechen damit auch nicht den Zielen der ISRM.
Im Rahmen dieses Beitrags sollen die auf Basis der o. g. Gebirgskennziffern eingeführten Entwurfsmethoden diskutiert werden, die international oft als prescriptive measures beschrieben werden.
Q-System
Nach dem Q-System werden die Eigenschaften des Felses durch den sogenannten Q-Wert beschrieben, der sich aus dem Produkt von sechs Konstanten ergibt (Bild 2). Als zweite Eingangsgröße für den Entwurf der Sicherung eines Tunnels werden der Durchmesser eines Tunnels und der sogenannte ESR (Excavation Support Ratio) benötigt, der aus Tabellen für verschiedene Bauwerkstypen abgeleitet werden kann. Aus dem Quotienten des Durchmessers und dem ESR errechnet man den Wert De. De und Q bilden die Eingangsgrößen für ein Nomogramm aus dem dann eine sogenannte Sicherungsklasse abgeleitet werden kann (Bild 2). Für diese Sicherungsklasse können die einzubauenden Sicherungsmittel aus Tabellen abgelesen werden. Weitergehende Berechnungen sowie Sicherheitsbetrachtungen im Sinne der Normung sind nicht vorgesehen.
Prof. Nick Barton führt in [11] aus, dass das Q-System auf das gesamte Spektrum von Gebirgsqualitäten anwendbar ist. Diese Aussage ist aus Sicht der Autoren allerdings aus mehreren Gründen nicht haltbar.
Zunächst muss festgehalten werden, dass das Nomogramm im Jahr 1974 auf der Grundlage von 212 Fallbeispielen aufgestellt wurde. Nur 19 dieser Tunnelprojekte lagen in Sedimentgesteinen. Es ist offensichtlich, dass diese geringe Zahl von Beispielen und die bei den Projekten gesammelten Erfahrungen in keiner Weise ausreichend sein können, die Zulässigkeit der Anwendung des Systems in allen Gebirgsverhältnissen zu begründen. Das gilt auch heute noch, obschon das Nomogramm in den 1990er-Jahren auf der Grundlage von mehr als 1000 Fallbeispielen weiterentwickelt wurde [18]. Auch hierbei handelte es sich bei näherem Hinsehen nahezu ausschließlich um Tunnelbauwerke im Kristallin.
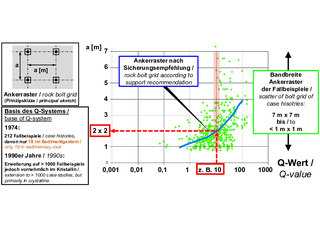3 | Sicherungsempfehlungen auf der Grundlage von Fallbeispielen [19]
Credit/Quelle: WBI GmbH
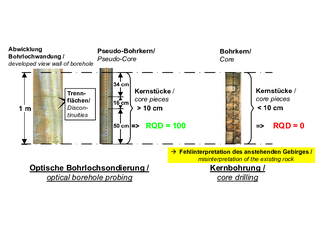4 | Einfluss der Kernqualität auf den RQD-Wert
Credit/Quelle: WBI GmbH
Dessen ungeachtet erscheint auch die Anwendbarkeit der Methode bei Tunnelbauwerken im Kristallin fragwürdig. Um diese Aussage zu belegen, ist im Bild 3 das Ankerraster dargestellt, dass sich nach der Sicherungsempfehlung gem. Barton für verschiedene Q-Werte ergibt (blaue Kurve). Nach Angaben in [19] basiert die Sicherungsempfehlung auf den durch die in Bild 3 mit grünen Punkten gekennzeichneten Fallbeispielen. Von einer Korrelation zwischen dem Q-Wert und dem angewendeten Ankerraster kann hier sicherlich nicht gesprochen werden.
Auch wenn allein diese Ausführungen zeigen, dass das Q-System den heutigen Anforderungen an die Tunnelplanung nicht genügt, sollen nachstehend noch weitere Risiken aufgezeigt werden, die sich aus der Anwendung des Systems ergeben können. Dazu sollen die verschiedenen Eingangsgrößen für die Ermittlung des Q-Werts näher betrachtet werden.
Die erste und bekannteste Eingangsgröße ist der sogenannte RQD-Wert [14]. Dieser ergibt sich aus der Länge der Stücke eines Bohrkerns mit einer Länge von > 10 cm dividiert durch die gesamte Bohrkernlänge. Er soll die „Felsqualität“ beschreiben.
Grundsätzlich kann der RQD-Index zwar einen ersten Anhaltswert für die Eigenschaften des Felses geben. Er hängt aber sehr stark von der Qualität der Bohrkerne und damit von der Sorgfalt des Bohrmeisters ab. Das kann man an dem Beispiel in Bild 4 erkennen. Während nach dem Kern (rechtes Bild) ein RQD-Wert von 0, d. h. eine sehr schlechte Felsqualität zu erwarten wäre, zeigt der in der gleichen Bohrung ausgeführte Bohrlochscan, dass nur zwei Trennflächen vorhanden sind, die zudem einen Abstand von mehr als 10 cm aufweisen. Der tatsächliche RQD-Index bei diesem Beispiel wäre somit 100 %.
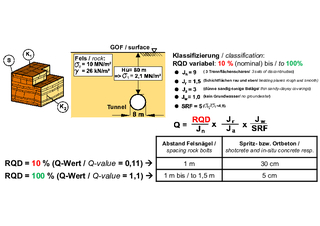5 | Einfluss des RQD-Index auf die Sicherungsempfehlungen gem. Q-System
Credit/Quelle: WBI GmbH
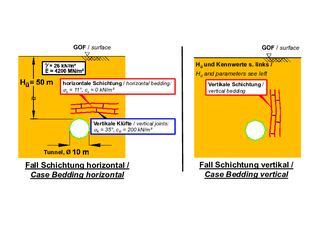6 | Einfluss der Raumstellung des Trennflächensystems auf die Sicherung, Aufgabenstellung
Credit/Quelle: WBI GmbH
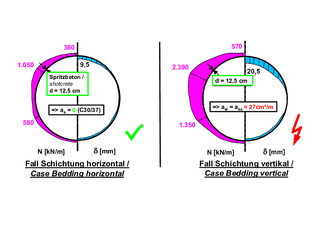7 | Einfluss der Raumstellung des Trennflächensystems, Ergebnis
Credit/Quelle: WBI GmbH
Die Auswirkung einer solchen Fehlinterpretation wären bei der Anwendung des Q-Systems erheblich. Bei sonst gleichen Annahmen würde man bei dem in Bild 5 dargestellten Beispiel für einen RQD von 10 einen Q-Wert von 0,11 erhalten, nach dem jeden Meter Anker erforderlich sind und die Laibung mit 30 cm Spritzbeton gesichert werden müsste. Für RQD = 100 % wären dagegen nach dem Nomogramm nur 5 cm Spritzbeton und ein größeres Ankerraster ausreichend.
Außer dem RQD-Index gehen noch fünf andere Konstanten in die Bestimmung des Q-Wertes ein (Bild 2, JN: Anzahl Trennflächenscharen; JR: Rauhigkeit; Ja: Ausbildung/ Füllung der Trennflächen; JW: Reduzierungsfaktor Grundwasser; SRF: Stress Reduction Factor). Die Anzahl der Trennflächenscharen Jn ist messbar. Alle übrigen Konstanten müssen über qualitative Beschreibungen aus Tabellenwerten abgeleitet werden. Anisotropien und die Raumstellung der Trennflächen bleiben im Q-System unberücksichtigt.
Dass diese Vereinfachung unzulässig ist, soll anhand des in Bild 6 dargestellten Beispiels gezeigt werden. Es wird ein im Sedimentgestein liegender Tunnel mit einem Durchmesser von 10 m betrachtet, der eine Überdeckung von 50 m aufweist. In dem im Bild 6 auf der linken Seite dargestellten Beispiel wird davon ausgegangen, dass die Schichtung horizontal verläuft, während die Schichtung im rechts dargestellten Fall vertikal sein soll. Die übrigen Annahmen sind in beiden Fällen gleich.
Nach der Sicherungsempfehlung des Q-Systems wäre in beiden Fällen eine 12,5 cm dicke Spritzbetonschale und 3,5 m lange Anker, die in einem Raster von 1 m x 1 m eingebaut werden, erforderlich. FE-Berechnungen nach der AJRM-Methode (s. Abschnitt 2) zeigen, dass diese Empfehlung für den Fall, dass die Schichtung horizontal liegt, ausreichend ist, während die 12,5 cm dicke Spritzbetonschale bei einer vertikal verlaufenden Schichtung deutlich überbeansprucht wäre. Bei einer Bemessung mit den Sicherheitsbeiwerten der außergewöhnlichen Bemessungssituation ergäbe sich in diesem Fall eine erforderliche Bewehrung von ~27 cm²/m innen und außen, die sich in eine 12,5 cm dicke Spritzbetonschale nicht einbauen lässt. Eine Sicherung nach dem Q-System würde in diesem Fall also zu einem Versagen des Ausbaus führen (Bild 7). Dieses Beispiel zeigt, dass die fehlende Berücksichtigung der Orientierung der Trennflächen im Q-System nicht zulässig ist und große Risiken beinhalten kann.
RMR- und RMi-Systeme
Die obenstehenden Ausführungen haben gezeigt, dass die Anwendung des Q-Systems für die Tunnelplanung in Sedimentgesteinen nicht zulässig ist und große Risiken beinhalten kann. Wie einleitend erwähnt, wurden in der Vergangenheit noch weitere Klassifizierungssysteme eingeführt.
8 | Weitere Klassifizierungssysteme
Credit/Quelle: WBI GmbH
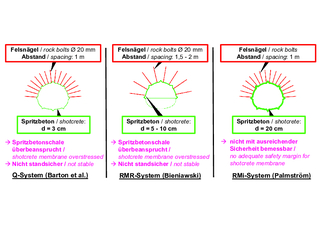9 | Fallbeispiel Österfeldtunnel, Sicherungsempfehlungen Q-, RMR- und RMi-System
Credit/Quelle: WBI GmbH
Das RMR-System von Bieniawski funktioniert grundsätzlich in der gleichen Weise wie das Q-System. Der RMR-Wert ergibt aus der Summe von insgesamt sechs Konstanten. Auf der Basis des RMR-Wertes können Sicherungsempfehlungen für Tunnelbauwerke aus Tabellen abgeleitet werden (Bild 8, linke Seite).
Auch das RMi-System basiert auf Empirie. Der RMi-Wert wird über eine etwas kompliziertere Formel berücksichtigt. Zusammen mit weiteren Kenngrößen, die sich aus Tabellen ableiten lassen, können auch hier Sicherungsempfehlungen aus Tabellen bzw. Nomogrammen ermittelt werden (Bild 8, rechts).
Auch die Anwendung dieser beiden Systeme, auf die hier nicht näher eingegangen werden soll, ist nach Auffassung der Autoren für Tunnelbau in Sedimentgesteinen ungeeignet. Diese Aussage soll anhand eines weiteren Beispiels verdeutlicht werden. Es handelt sich hierbei um den vor vielen Jahren gebauten Österfeldtunnel in Stuttgart, der im Schwarzjura liegt [20].
Die Planung und der Bau des Tunnels erfolgten nach der AJRM-Methode. Dabei wurden das anisotrope Verformungsverhalten und die verminderten Festigkeiten entlang der Schichtung und der Klüfte in den mit der Methode der finiten Elemente geführten statischen Berechnungen berücksichtigt. Der Bau wurde messtechnisch begleitet. Die Rechenannahmen wurden anhand der Messergebnisse überprüft. Nach dem Bau wurden zum Vergleich die Sicherungsempfehlungen nach dem Q-System, nach dem RMR-System und nach dem RMi-System abgeleitet. Zunächst bleibt festzustellen, dass alle drei Systeme zu deutlich voneinander abweichenden Sicherungsempfehlungen kommen (Bild 9).
Ein Vergleich mit der Ausführung und entsprechenden Nachrechnungen hat zudem gezeigt, dass eine Ausführung nach dem Q-System zu einem Versagen des Bauwerks geführt hätte. Auch nach dem RMR-System wäre der Tunnel vermutlich eingestürzt. Wenn eine Planung nach dem RMi-System erfolgt wäre, wäre zwar nichts passiert, die geforderten Sicherheiten wären jedoch nicht eingehalten gewesen.
4 Fallbeispiel Tunnel Trimberg, Autobahn A44
Leider werden die in Abschnitt 3 behandelten Klassifizierungssysteme bzw. die zugehörigen Gebirgskennziffern trotz der beschriebenen Unzulänglichkeiten, in jüngerer Vergangenheit auch in Deutschland angewendet bzw. werden entsprechende Angaben in Gutachten gemacht. Im tunnelbautechnischen Gutachten für den Tunnel Trimberg an der A44 finden sich neben den felsmechanischen Kennwerten auch Angaben zum RMR-Wert.
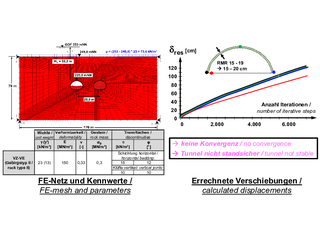10 | Tunnel Trimberg, Abschnitt im Netra-Graben, FE-Berechnungen für den Bauzustand mit offener Kalottensohle
Credit/Quelle: WBI GmbH
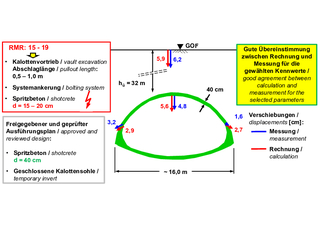11 | Tunnel Trimberg, Abschnitt im Netra-Graben, Vortrieb mit temporärer Sohle, Vergleich der gemessenen und der prognostizierten Verschiebungen
Credit/Quelle: WBI GmbH
Die Bedeutung dieses Werts haben wir beispielsweise für den Tunnelabschnitt im Netra-Graben näher untersucht. Der Tunnel hat hier eine Überdeckung von 32 m und der im Gutachten angegebene RMR-Wert beläuft sich auf 15 bis 19.
Für diese Werte ergibt sich aus dem RMR-System, dass der Tunnel im Kalottenvortrieb mit Abschlaglängen von 50 cm bis 1 m, mit einer Systemankerung und 15 bis 20 cm Spritzbeton aufgefahren werden kann (Bilder 10 &11).
Berechnungen nach der AJRM-Methode (Abschnitt 2) unter Berücksichtigung der elastischen und viskoplastischen
Gesteinseigenschaften und der Trennflächen zeigen, dass ein entsprechender Tunnelvortrieb nicht standsicher wäre. Die Berechnungen zeigen keine Konvergenz (Bild 10). Vielmehr war ein Kalottenvortrieb mit einer geschlossenen Sohle und eine 40 cm dicke Spritzbetonschale erforderlich (Bild 11). Die Anwendung der RMR-Methode mit den zugehörigen Werteangaben
im Tunnelbautechnischen Gutachten hätte somit zu einem Versagen geführt. Die Anwendung der AJRM-Methode unter Berücksichtigung der felsmechanischen Modelle und entsprechender Berechnungen führte dagegen zu einem sicheren und wirtschaftlichen Tunnelbau. Das kann auch durch einen Vergleich der errechneten (prognostizierten) und der gemessenen Verschiebungen gezeigt werden (Bild 11).
5 Schlussfolgerungen
Nach Ansicht der Autoren muss davor gewarnt werden, die sogenannten prescriptive measures in Form des Q-Systems, des RMR-Systems oder des RMi-Systems bei der Tunnelplanung zu verwenden. Die unzulässige Vereinfachung der Beschreibung des Felses durch einzelne Gebirgskennziffern ist irreführend und führt zu großen Risiken. Bei Anwendung der Nomogramme und Tabellen werden keine Standsicherheitsnachweise geführt. Auch deshalb ist die Anwendung dieser Methoden in Deutschland nach aktueller Vorschriftenlage nicht zulässig. Wir hoffen, dass das auch nach der in Kürze zu erwartenden Einführung des neuen EC 7 so bleibt. In der Fachwelt sollte besser gemeinsam weiter daran gearbeitet werden, die AJRM-Methode weiterzuentwickeln als Energie in die Weiterentwicklung von Systemen zu stecken, die aus Sicht der Autoren dieses Beitrags schon in der Grundlage nicht richtig sind.
