Maschinelle Vortriebe in klüftigem Fels

Credit/Quelle: WBI

1 Interaktion Fels – Tunnelvortriebsmaschine – Tübbingauskleidung

1.1 Aufgabenstellung

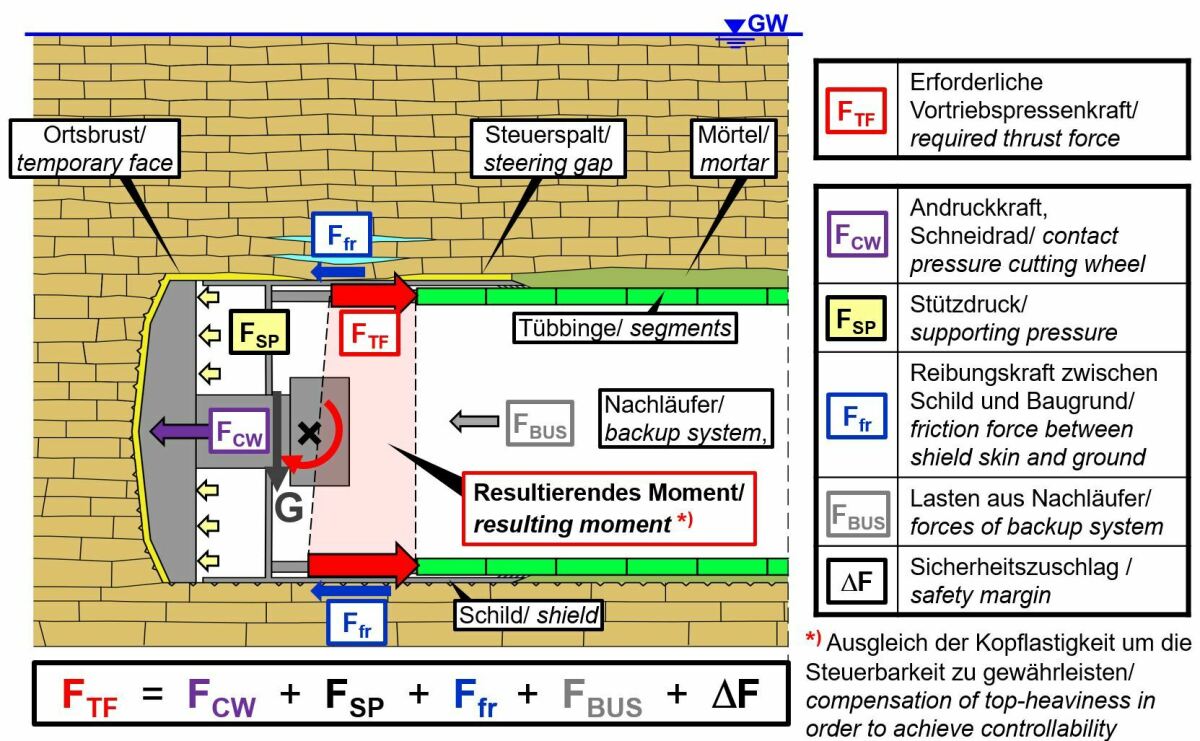
Beim maschinellen Vortrieb ist ein komplexes Zusammenspiel aus Einwirkungen und erforderlichen Kräften zu beachten (Bild 1):

Die Ortsbrust muss gegen die Einwirkungen aus Gebirgs- und Wasserdruck bzw. Strömungsdruck gestützt werden. Hierzu dienen die Andruckkraft des Bohrkopfs F_CW sowie etwaige Stützdrücke F_SP. Beide müssen mithilfe der Vortriebspressenkräfte F_TF aufgebracht werden.

Gleichzeitig dient die Ortsbrust als Widerlager. Sie muss ausreichend „kompetent“ sein, damit die Vortriebspressenkräfte aufgebracht werden können. Ist dies nicht gegeben und besteht keine Möglichkeit, dies auf andere Weise zu kompensieren, so kommt es zu einem Abfallen der Vortriebspressenkräfte (vgl. Kap. 1.4.5).

Die Andruckkraft des Bohrkopfs F_CW sowie das Drehmoment müssen ausreichend groß bemessen sein, um ein Lösen des Felses zu ermöglichen.

Die Reibungskräfte zwischen Schild und Baugrund F_fr müssen überwunden werden. Auch hierfür müssen die Vortriebspressenkräfte F_TF ausreichend bemessen werden.

Auch die Anhängelast des Nachläufers F_BUS muss mit den Vortriebspressenkräften bewegt werden. 1| Zusammenwirken von TBM, Tübbingauskleidung und Gebirge
Credit/Quelle: WBI

Damit müssen die Vortriebspressenkräfte unter Berücksichtigung eines Sicherheitsaufschlags ΔF so bemessen sein, dass sie die erforderliche Andruckkraft F_CW, den Stützdruck F_SP, sowie die Überwindung der Reibungskräfte F_fr und der Anhängelast des Nachläufers F_BUS gewährleisten können (Kräftegleichgewicht in horizontaler Richtung, Bild 1).

Die Vortriebspressen stützen sich gegen den Tübbingring ab. Die Tübbinge müssen gegen die zu erwartende maximale Vortriebspressenkraft bemessen werden. Gleichzeitig ist ein Mindestwert der Vortriebspressenkraft auf die Tübbingringe zu gewährleisten, um die Vorspannung der Dichtungsprofile in den Ringfugen zu erhalten und damit die Dichtigkeit der Tübbingringe sowie die Lagesicherheit der ersten, „schwebenden“ Tübbingringe zu garantieren.

Da die Tunnelvortriebsmaschinen (TVM) in der Regel kopflastig sind, ergibt sich als zusätzliche Forderung, dass im Sohlbereich größere Vortriebspressenkräfte aufgebracht werden als im Firstbereich. Hieraus ergibt sich ein Moment, das die Kopflastigkeit ausgleicht und damit eine planmäßige Steuerung der TVM erlaubt (Bild 1). Dies ist jedoch nur dann möglich, wenn – wie bereits erwähnt – die Ortsbrust ein ausreichend kompetentes Widerlager bietet oder, falls dies nicht der Fall ist, angemessene Maßnahmen zur Kompensation ergriffen werden (vgl. Kap. 1.4.5). 

1.2 Eigenschaften von klüftigem Fels

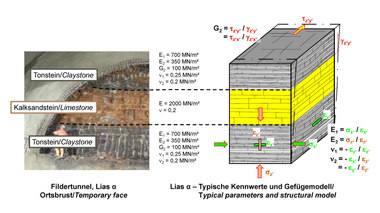
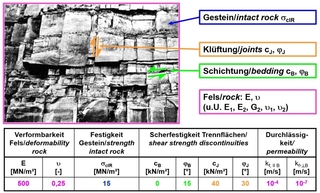
Klüftiger Fels lässt sich mit dem „Anisotropic Jointed Rock Model (AJRM)“, das seit vielen Jahren erfolgreich angewendet wird, in seinen wesentlichen Eigenschaften erfassen und nachbilden. Eine nähere Beschreibung des AJRM findet sich z. B. in [1, 2, 3, 4]. Bild 2 zeigt ein typisches Beispiel eines Sedimentgesteins mit annähernd horizontalen Schichtfugen, die teilweise mit Ton gefüllt sind, und steil stehender Klüftung. Die Klüfte setzen häufig an den Schichtfugen ab. Das Festigkeits- und Verformungsverhalten des Felses wird vom Gestein und von den Trennflächen bestimmt.

Für Beanspruchungen unterhalb der Festigkeit kann man bei den meisten Felsarten näherungsweise von linear-elastischem Verhalten ausgehen. Sedimentgesteine, Tonschiefer und auch Gneise verhalten sich aber im elastischen Bereich nicht immer isotrop. Vielmehr ist die Zusammendrückbarkeit senkrecht zur Schichtung oder Schieferung häufig größer als parallel dazu. Diese Eigenschaft kann in guter Näherung durch die Annahme einer transversalen Isotropie mit Hilfe von fünf elastischen Konstanten beschrieben werden: die E-Moduln parallel und senkrecht zur Schichtung E₁ und E₂, zwei Poisson’sche Zahlen ν₁ und ν₂ und den Schubmodul G₂. In dem in Bild 2 dargestellten Fall kann näherungsweise von einem elastisch isotropen Verformungsverhalten ausgegangen werden, welches durch den E-Modul und die Querkontraktionszahl beschrieben werden kann.

Hinsichtlich der Festigkeit wird unterschieden zwischen der Festigkeit des unzerklüfteten Gesteins σ_cIR und der Scherfestigkeit auf den Trennflächen (Schichtfugen, Klüfte), die in der Praxis durch einen Reibungswinkel φ_B / φ_J und eine Kohäsion c_B / c_J beschrieben werden können. Die Scherfestigkeiten auf den Trennflächen sind in der Regel erheblich kleiner als die Gesteinsfestigkeit und damit maßgeblich für die Standsicherheit von Felsbauwerken.

Aufgrund der unterschiedlichen Ausbildung der Trennflächen ist häufig auch die Durchlässigkeit des Felses parallel und senkrecht zur Schichtung verschieden und damit anisotrop. 2| Felsmechanisches Modell
Credit/Quelle: WBI

Die Tabelle in Bild 2 zeigt beispielhaft typische Kennwerte eines Buntsandsteins mit einer ausgeprägten Anisotropie der Festigkeit und auch der Durchlässigkeit.

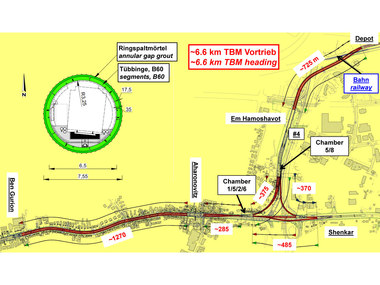
Die nachstehenden rechnerischen Betrachtungen werden für das Beispiel eines maschinellen Vortriebs in einem Buntsandstein mit diesen Kennwerten (Bild 2) bei einer Überlagerung von etwa 40 m oberhalb der Tunnelfirste sowie einem an der Geländeoberfläche anstehenden Grundwasserspiegel durchgeführt (vgl. Bild 1). 

1.3 Grundwasser und Sickerströmung

Wenn ein Tunnelvortrieb unterhalb des Grundwasserspiegels durchgeführt wird und Wasser im Bereich der Ortsbrust und des Schildes eintreten kann, dann wird eine zum Tunnel gerichtete Sickerströmung ausgelöst. In diesem Fall, der den nachstehenden Betrachtungen zugrunde liegt, wirken auf den Fels Strömungs- und Auftriebskräfte. Wenn im Bereich des Schildes oder über die Ortsbrust kein Wasser eintreten kann, dann wirkt der volle Wasserdruck auf Ortsbrust, Schild und Tübbingauskleidung, und im Fels wirken die Auftriebskräfte.

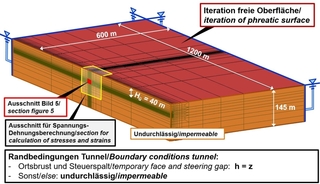
Die entsprechenden Einwirkungen können mit Hilfe von Sickerströmungsberechnungen ermittelt werden. Solche Berechnungen wurden für den Beispielfall mit dem in Bild 3 dargestellten FE-Netz durchgeführt. Im Falle einer Sickerströmung ändert sich die Potentialverteilung weiträumig. Deshalb ist für diese Berechnungen ein großer Berechnungsausschnitt (600 m x 1200 m x 145 m) erforderlich. Die Randbedingungen sind im Einzelnen in Bild 3 dargestellt. 3| FE-Netz und Randbedingungen für die Sickerströmungsberechnungen
Credit/Quelle: WBI

4| Sickerströmungsberechnung, Längsschnitt mit Potentiallinienverteilung
Credit/Quelle: WBI

4| Sickerströmungsberechnung, Längsschnitt mit Potentiallinienverteilung

Credit/Quelle: WBI

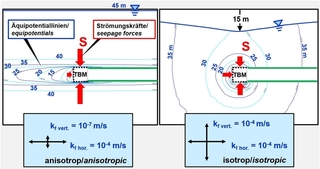
Bild 4 zeigt die errechneten Potentiallinienverteilungen im Nahbereich des Tunnels, die sich infolge der zum Tunnel gerichteten Sickerströmung ergeben. Bei Annahme einer anisotropen Durchlässigkeit des Felses (k_fh >> k_fv, siehe Bild 2) ergibt sich eine deutliche Konzentration der Potentiallinien und damit des Gefälles ober- und unterhalb des Schildes und der Tübbingauskleidung (Bild 4, links). In der Folge wirken in vertikaler Richtung deutlich höhere Sickerströmungskräfte (S) als in horizontaler Richtung. Darüber hinaus stellt sich praktisch keine Absenkung des Grundwasserspiegels an der Geländeoberfläche ein.

Zum Vergleich ist in Bild 4 rechts die Potentiallinienverteilung dargestellt, die sich bei isotroper Durchlässigkeit des Felses ergibt: in diesem Fall stellt sich eine deutliche und weitreichende Absenkung des Grundwasserspiegels an der Geländeoberfläche ein. Die Potentiallinienverteilung um den Tunnel ist annähernd symmetrisch, die Strömungskräfte in vertikaler Richtung sind deutlich geringer, die zur Ortsbrust gerichteten Strömungskräfte hingegen größer als im Falle anisotroper Durchlässigkeit.

Diese Ergebnisse zeigen sehr deutlich, dass die Anisotropie der Durchlässigkeit einen großen Einfluss sowohl auf die Krafteinwirkungen im Bereich von Ortsbrust, Schild und Tübbingauskleidung als auch auf die Änderungen des Grundwasserspiegels an der Geländeoberfläche hat. Ein Effekt, der in der Planung und Ausführung nicht vernachlässigt werden darf. 

1.4 Spannungen und Verformungen

1.4.1 Berechnungsausschnitt und FE-Netz

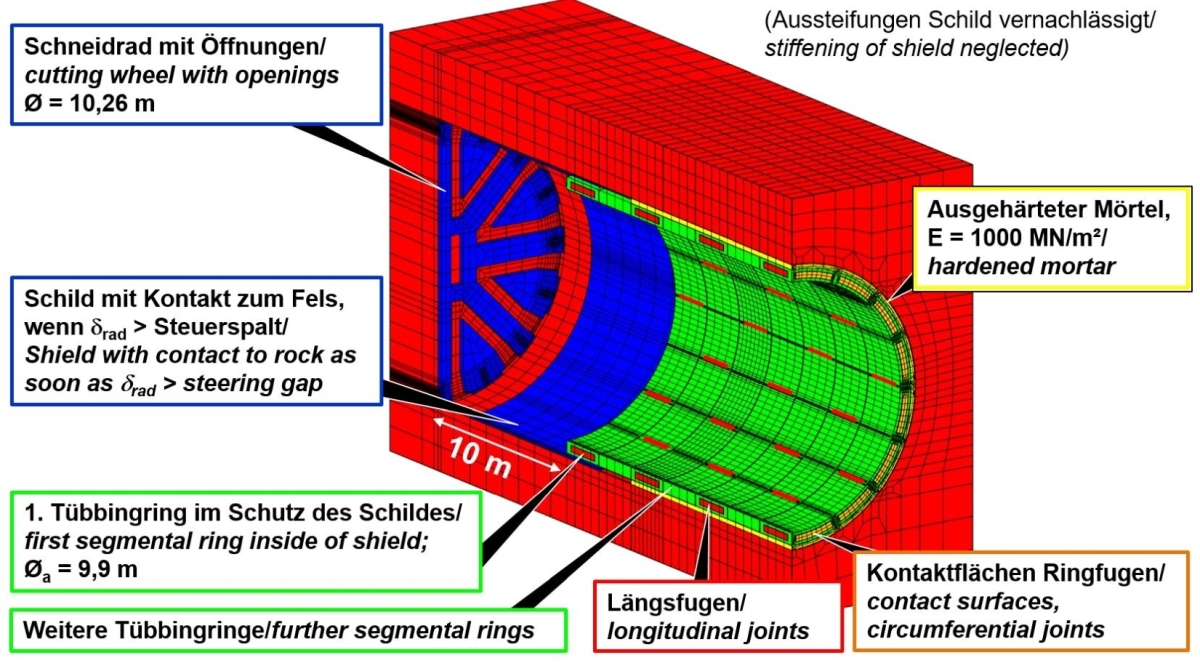
Für die Berechnung der Spannungen und Verformungen reicht ein deutlich kleinerer Berechnungsausschnitt (vgl. gelbe Kennzeichnung in Bild 3). Neben dem Fels werden in dem verwendeten FE-Netz sowohl das Schneidrad mit Öffnungen, als auch der Vortriebsschild und die Tübbingringe im Detail nachgebildet (vgl. Detail des FE-Netzes in Bild 5; Lage des Details: siehe rotes Rechteck in Bild 3).

5| FE-Netz, Detail
Credit/Quelle: WBI

Zwischen dem Vortriebsschild und dem Gebirge wird zu Beginn der Berechnung ein offener Steuerspalt simuliert, der in dem betrachteten Fall in der Firste 4 cm und in der Sohle 2 cm dick ist. Der erste Tübbingring befindet sich noch im Schutze des Schildes und ist somit nicht im Ringspaltmörtel gebettet. Der zweite Tübbingring ist in noch nicht erhärtetem Ringspaltmörtel gebettet. In der Rechnung wird der Mörteldruck berücksichtigt. Die folgenden Tübbingringe sind im erhärteten Ringspaltmörtel gebettet. Das Eigengewicht der ersten beiden Tübbingringe muss durch Reibungskräfte in den Ringfugen zwischen erstem, zweiten und dritten Tübbingring gehalten werden. Dazu sind entsprechende Vortriebspressenkräfte erforderlich. 

1.4.2 Annahmen und Berechnungsschritte

Es wurde der bereits erläuterte Beispielfall betrachtet (vgl. Kap. 1.2). In einer vorgelagerten Sickerströmungsberechnung wurden – unter der Annahme, dass Grundwasser im Bereich der Ortsbrust und des Schildes zuströmen kann – die Auftriebs- und Strömungskräfte ermittelt (vgl. Kap. 1.3). Diese werden in den Berechnungen der Spannungen und Verformungen als Lasten berücksichtigt.

Die Berechnungen der Spannungen und Verformungen werden in insgesamt zehn Rechenschritten ausgeführt. Der erste Rechenschritt dient derSimulation des In-Situ-Spannungszustands. In den Rechenschritten 2 und 3 werden Ausbruch und Sicherung eines 85 m langen Tunnelabschnitts nach dem Stützkernverfahren simuliert. Das Ergebnis bildet den Ausgangszustand für die nachfolgende Berechnung eines schrittweisen Vortriebs in den Rechenschritten 4 bis 10. In jedem dieser Rechenschritte wird der Vortrieb eines 2 m langen Tunnelabschnitts simuliert. Dabei werden berücksichtigt: das Schneidrad mit Anpressdruck an der Ortsbrust, der Vortrieb, der Bau des Tübbingrings, die Lagesicherung des Tübbingrings mit Hilfe der Vortriebspressenkräfte, der Mörtelverpressdruck im Bereich des zuvor eingebauten Tübbingrings, der erhärtete Mörtel im Bereich der weiter zurückliegenden Tübbingringe. 

1.4.3 Stützung der Ortsbrust

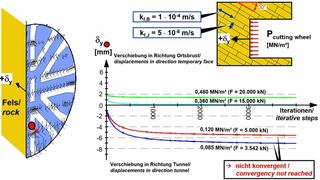
In einer der Berechnungen wurde angenommen, dass die Schichtung unter einem Winkel von 30 ° in die Ortsbrust einfällt (Bild 6). Ansonsten gelten die Annahmen des Beispielfalls.

In den Berechnungen wurde der Anpressdruck des Schneidrads gegen die Ortsbrust variiert. Es zeigte sich, dass resultierende Kräfte von 3542 kN und 5000 kN nicht ausreichen, um die Ortsbrust zu stabilisieren. Um die Standsicherheit der Ortsbrust unter den getroffenen Annahmen gewährleisten zu können, wären rechnerisch Kräfte von 15 000 bis 20 000 kN erforderlich (Bild 6). Dies macht deutlich, dass derlei Betrachtungen zur Standsicherheit der Ortsbrust unter Berücksichtigung der Raumstellung der Trennflächen, der Anisotropie der Festigkeit und der Durchlässigkeit sowie der Sickerströmung wichtig sind für die richtige Auslegung der Tunnelvortriebsmaschine für den Vortrieb im klüftigen Fels. 6| Einfluss des Anpressdrucks auf die Verschiebungen der Ortsbrust
Credit/Quelle: WBI

7| Hallandsås-Tunnel, Gründe für Standsicherheitsprobleme an der Ortsbrust
Credit/Quelle: [5]

7| Hallandsås-Tunnel, Gründe für Standsicherheitsprobleme an der Ortsbrust

Credit/Quelle: [5]

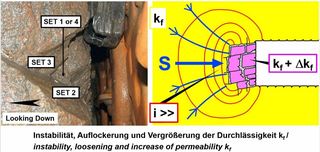
Ein Beispiel aus der Praxis, bei dem ein sehr hoher Grundwasserstand und der daraus resultierende Strömungsdruck zu Problemen im Hinblick auf die Standsicherheit der Ortsbrust führte, ist der auf der Bahnstrecke von Malmö nach Göteborg liegende Tunnel Hallandsås (Bild 7). Nähere Angaben hierzu finden sich in [5]. 

1.4.4 Belastung des Schildmantels und der Tübbingauskleidung

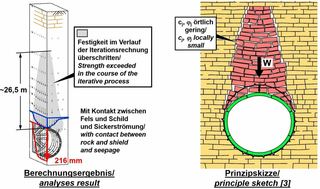
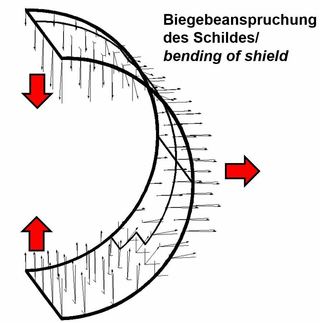
In weiteren Berechnungen wurde eine horizontale Schichtung angenommen. Ansonsten gelten die Annahmen des Beispielfalls. Diese Berechnungen zeigen, dass sich ein etwa 26 m hoher Felsblock auf den Schildmantel und somit auch auf die nachgelagerten Tübbingringe auflegt (Bild 8, links). Das rechts von dem Rechenergebnis skizzierte Prinzipbild veranschaulicht den durch die Schichtung und Klüftung verursachten Vorgang, der auch mit Beobachtungen von Nachbrüchen bei konventionellen Tunnelvortrieben im Sedimentgestein übereinstimmt. Dabei schließt sich der Steuerspalt im Firstbereich, und der Schildmantel verformt sich unter der Belastung des Felsblocks (Bild 9). Die Tübbingringe erfahren in den verschiedenen Bauzuständen die in Bild 10 dargestellten Verschiebungen, die man superponieren muss, um das endgültige Verschiebungsbild zu erhalten. Die daraus resultierenden Momenten- und Normalkraftverläufe sind in Bild 11 dargestellt. Der Ordnung halber sei erwähnt, dass die in den Längsfugen aufgrund der begrenzten Lastübertragungsfläche wirkenden Spannungskonzentrationen, gegen die die Tübbinge mit einer entsprechenden Spaltzugbewehrung zu bemessen sind, hier nicht dargestellt sind. 8| Verschiebungen und Bereiche mit Überschreitung der Festigkeit auf den Trennflächen
Credit/Quelle: WBI, [3]

9| Verformung des Schildmantels unter Belastung
Credit/Quelle: WBI

9| Verformung des Schildmantels unter Belastung

Credit/Quelle: WBI

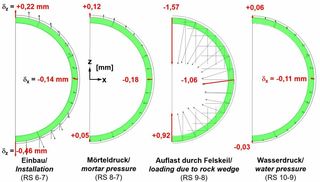10| Tübbingring 4, Vorderseite, Verschiebungen im Verlauf der Rechenschritte
Credit/Quelle: WBI

10| Tübbingring 4, Vorderseite, Verschiebungen im Verlauf der Rechenschritte

Credit/Quelle: WBI

11| Normalkräfte und Biegemomente im 4. Tübbingring
Credit/Quelle: WBI

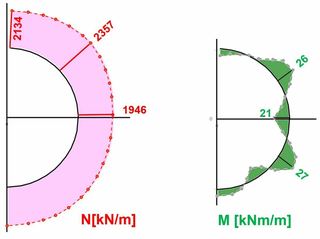11| Normalkräfte und Biegemomente im 4. Tübbingring

Credit/Quelle: WBI

Zum Vergleich wurden auch Berechnungen unter Annahme eines Gebirges ohne Grundwasser durchgeführt. Die resultierenden Verschiebungen sind in diesem Fall deutlich kleiner, jedoch immer noch so groß, dass sich der Steuerspalt schließt und der Schild belastet wird. Auch in diesem Fall bildet sich ein Felskeil oberhalb der Firste aus, der allerdings nur etwa halb so hoch reicht, wie beim Zusammenwirken mit einem Strömungsdruck bei anisotroper Wasserdurchlässigkeit.

In den Empfehlungen des DAUB für statische Berechnungen von Schildvortriebsmaschinen [6] wird – neben der ­Forderung, dass Lastannahmen entsprechend den Aussagen des Gutachtens projektspezifisch festzulegen sind – für Vortriebe „in horizontal geschichtetem Gebirge mit der Gefahr von „Sargdeckelbildung“ (Ausbildung eines Bruchkörpers entlang der Schicht- und Kluftflächen im Firstbereich)“ vorgegeben, dass „als Zusatzlastfall eine schlaffe Auflast auf den Schildmantel berücksichtigt werden“ muss. „Die vertikale Auflast infolge dieses Bruchkörpers sollte mindestens zu σ_V = 0,5 * D * γ_Fels (…) angesetzt werden.“ Dies entspricht einem Felskeil von etwa 5 m Höhe, was deutlich weniger ist als sich aus den vorstehend erläuterten Berechnungen mit und auch ohne Einfluss von Grundwasser ergibt.

Eine genauere rechnerische Betrachtung ist also notwendig und wichtig für die richtige Bemessung des Vortriebsschildes sowie der Tübbingauskleidung.  

1.4.5 Einleitung der Vortriebspressenkräfte in den Tübbingring

Wie in Kapitel 1.1 erläutert, dienen die Tübbingringe als Widerlager für die Vortriebspressen. Die Kräfte werden von den Vortriebspressen an die in den Ringfugen angeordneten Kontaktflächen abgegeben und führen dort zu Spannungskonzentrationen, die ihrerseits zu Spaltzugkräften in den Tübbingen führen (wie es Bild 12 für ein Projektbeispiel [3, 7] zeigt) . Um die Tübbinge entsprechend bemessen zu können, müssen die maximalen Vortriebskräfte, die sich aus den in Bild 1 dargestellten Anteilen zusammensetzen, in der Planungsphase ermittelt werden. In dem in Kapitel 1.4.4 betrachteten Fall tragen auch Kraftanteile, die zur Überwindung der Reibung des eingeklemmten Schildes erforderlich sind, erheblich zur Größe der Vortriebspressenkräfte bei.

Auf der anderen Seite erfordern die Dichtungen in den Ringfugen zwischen den Tübbingringen eine Vorspannung, aus der sich Mindest-Vortriebspressenkräfte ableiten lassen, die nicht unterschritten werden dürfen.

Wie bereits erwähnt, muss auch die Ortsbrust ein ausreichendes Widerlager bieten, um die Vortriebspressenkräfte aufbringen zu können. Den Autoren sind aus der Praxis verschiedene Fälle von maschinellen Vortrieben im EPB-Modus im klüftigen Fels bekannt, bei denen die Gebirgsfestigkeit an der Ortsbrust derartig gering war und/oder die Standsicherheit an der Ortsbrust nicht gegeben war, so dass diese Kräfte nicht aufgebracht werden konnten. Die Vortriebspressenkräfte fielen in der Folge wiederholt ab, es kam zu Problemen bei der Steuerung der Tunnelvortriebsmaschine sowie bei der Lagesicherung und Dichtigkeit der Tübbingringe. Es musste eine ergänzende Druckluftstützung (EPB & Teilfüllung & Druckluft) vorgesehen werden, um einen einwandfreien Vortrieb zu ermöglichen. Entsprechende Beobachtungen wurden beispielsweise in einem Abschnitt des Neuen Schlüchterner Tunnels in den Schichten des oberen Buntsandsteins gemacht [8].

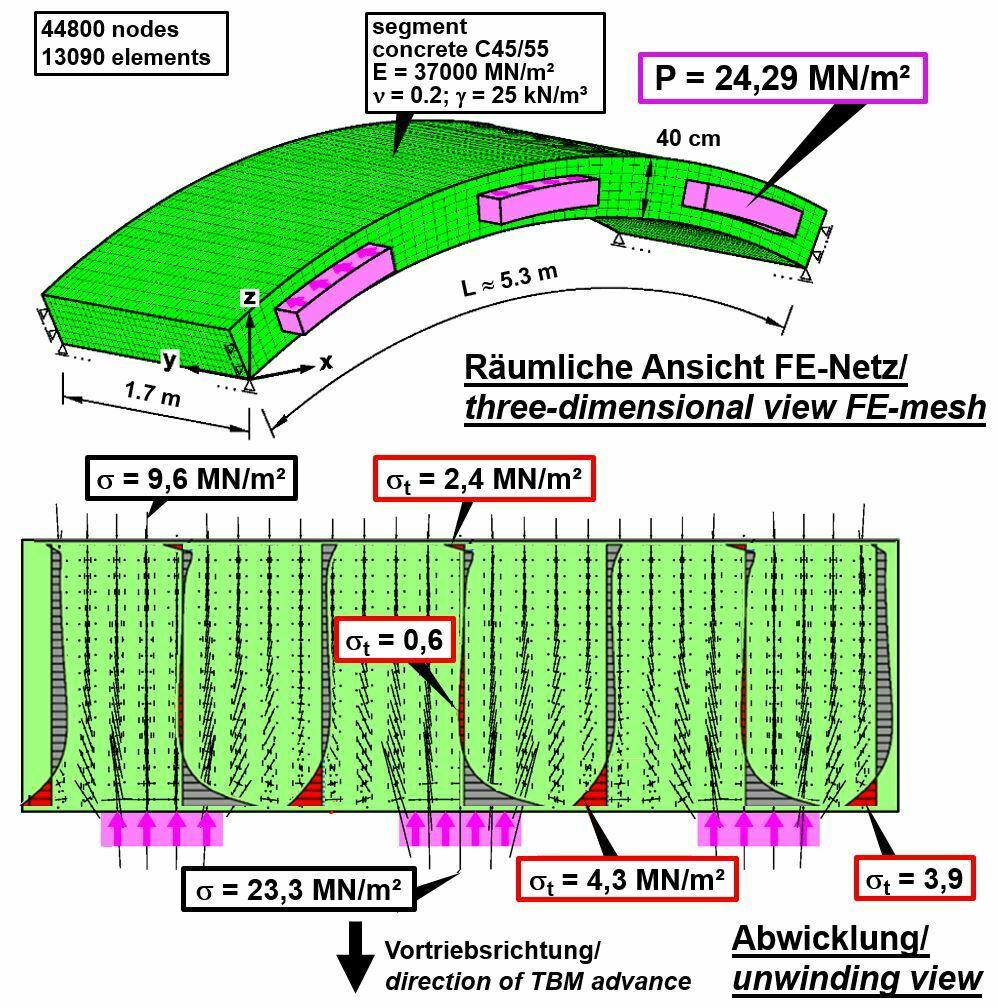  12| Spaltzugkräfte aus Vortriebspressenkräften für ein Projektbeispiel
Credit/Quelle: [3, 7]

2 Betrachtungen zum Ringspaltmörtel

2.1 Bi-Komponentenmörtel

Die Verwendung von Bi-Komponentenmörtel zur Ringspaltverfüllung hat aus baubetrieblicher Sicht sowie hinsichtlich des Mörtelauftriebs Vorteile. Für Tunnelvortriebe im Fels ist er jedoch aus Sicht der Autoren in den meisten Fällen nicht geeignet, da aus folgenden Gründen eine vollständige Füllung des Ringspalts, die für die Bettung des Tübbingrings erforderlich ist, nicht gewährleistet werden kann:

Man kann oder muss davon ausgehen, dass der Hohlraum im Bereich des Vortriebsschildes zumindest bereichsweise standsicher ist. In diesem Fall bleibt der Steuerspalt in der Firste offen. In der Folge kann der Bi-Komponentenmörtel nach vorne zur Ortsbrust abfließen. In der Folge lässt sich kein Verpressdruck aufbauen, und der Ringspalt bleibt im Firstbereich offen.

Ein Beispiel aus der Praxis, bei dem dies beobachtet wurde, ist der Boßlertunnel, der im Zuge der NBS Stuttgart–Ulm mit einer Tunnelvortriebsmaschine aufgefahren wurde. Hier wurden im Nachgang zum Vortrieb umfangreiche Nachverpressungen im Firstbereich erforderlich (Bild 13, [9, 10]).

Darüber hinaus können die Trennflächen in Sedimentgesteinen, wie z. B. Sandsteinen, bereichsweise Öffnungsweiten haben, über die der Bi-Komponentenmörtel ebenfalls abfließen kann. Auch deshalb kann eine vollständige Füllung des Ringspalts mit Bi-Komponentenmörtel nicht gewährleistet werden.

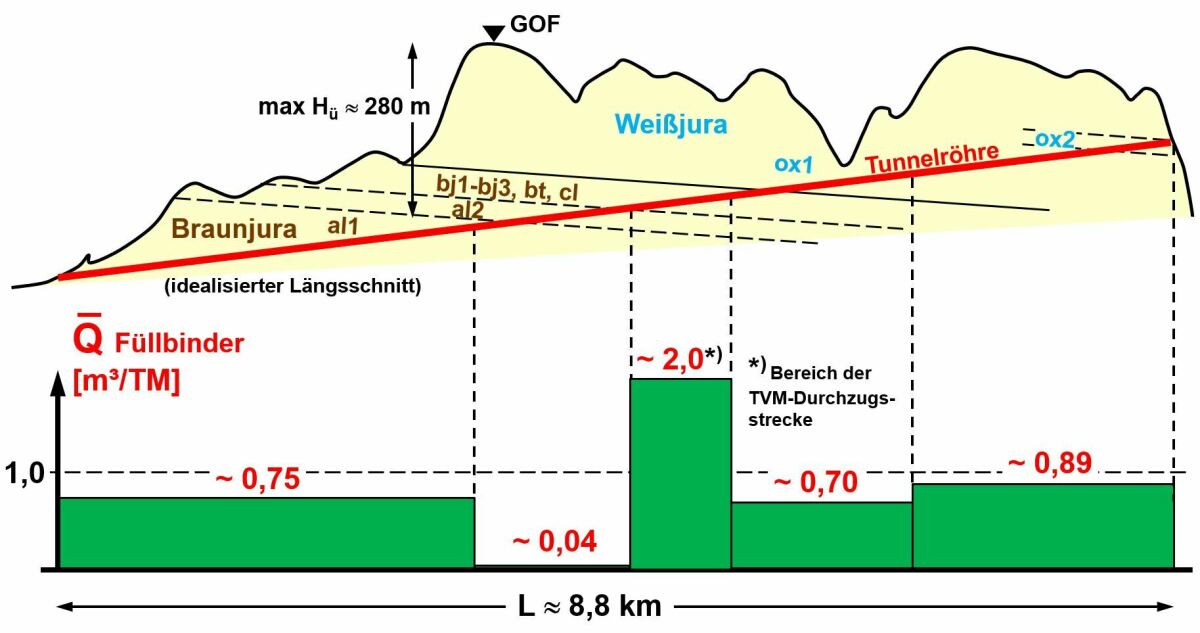  13| Bi-Komponenten-Mörtel, Mittlere Aufnahmemengen bei der Nachverfüllung des Ringspalts der Oströhre des Boßlertunnels
Credit/Quelle: WBI

2.2 Zementmörtel

Zementmörtel zur Ringspaltverpressung besitzen in der Regel geringe Zementanteile mit einem hohen W/Z-Faktor. Die Folge dieser Zusammensetzungen sind geringe E-Moduln, die sich zudem nur langsam entwickeln. Die vollständige Bettung des Tübbingrings stellt sich deshalb möglicherweise erst in größerem Abstand zur temporären Ortsbrust ein. Darüber hinaus ist die zeitliche Entwicklung des E-Moduls von den Dränagebedingungen und damit von dem k_f-Wert des Baugrunds abhängig. So entwickelt sich der Steifemodul eines Mörtels mit 50 kg/m³ Zementanteil wesentlich günstiger bei dränierten als bei undränierten Bedingungen (Bild 14, [11, 3]). 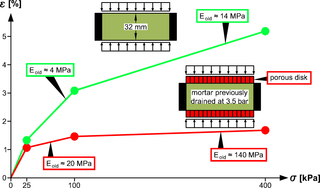14| Oedometer Test an Zementmörtel im dränierten und undränierten Zustand
Credit/Quelle: [11, 3]

Für ein Projekt in Israel konnte mit Ödometerversuchen an einem Zementmörtel unter dränierten Bedingungen gezeigt werden, dass schon der frische, noch nicht abgebundene Mörtel einen für die Bettung in diesem Fall ausreichenden E-Modul von 5 MPa aufweist, wenn der effektive Mörtelverpressdruck mindestens 1 bar beträgt und über einen gewissen Zeitraum aufrecht erhalten wird, um die Konsolidation des Mörtels zu ermöglichen (Bild 15, [12]). Der Baugrund muß in diesem Fall ausreichend durchlässig sein, um die Wasserabgabe des Mörtels zu ermöglichen. Es sei darauf hingewiesen, dass der für die Bettung erforderliche E-Modul sowie auch der für die Verpressung erforderliche effektive Mörtelverpressdruck projektspezifisch unter Berücksichtigung der jeweils vorliegenden Randbedingungen bestimmt werden müssen (vgl. hierzu sowie zu weiteren Anforderungen an den Ringspaltmörtel [13]).

15| Oedometer-Test an Zementmörtel
Credit/Quelle: [12]

Im Falle geringer Durchlässigkeiten des Baugrunds (undränierte Bedingungen) muss versuchstechnisch nachgewiesen werden, dass der Mörtel auch ohne Wasserabgabe abbindet. In diesem Fall ist es beim Vortrieb besonders wichtig, einen ausreichend großen Mörtelverpressdruck aufzubringen und über einen gewissen Zeitraum konstant zu halten, um hydrostatische Bedingungen zu erzeugen. Ist dies sichergestellt, so kann in vielen Fällen auch dann eine ausreichende Bettung der Tübbingringe bis zum Abbinden des Mörtels erreicht werden.

Besondere Betrachtungen werden allerdings erforderlich, wenn Verhältnisse zu erwarten sind, bei denen im Tunnelquerschnitt Schichten verschiedener Durchlässigkeit anstehen, so dass unterschiedliche Dränagebedingungen vorliegen, die zu einer ungleichmäßigen Bettung führen können. Dies kann z. B. bei den in Sedimentgesteinen häufigen Wechselfolgen aus gering durchlässigen Tonsteinen und stärker durchlässigen Sandsteinen der Fall sein.

Um ein Aufschwimmen der Tübbingringe zu verhindern, muss der Mörtel eine Mindest-Scherfestigkeit aufweisen ([13, 14]). Dies ist mit der Zusammensetzung sicherzustellen und versuchstechnisch nachzuweisen. 

3 Lösen des Gesteins

3.1 Abrasivität

Für Tunnelvortriebe im klüftigen Fels sind die gängigen Versuche zur Bestimmung der Abrasivität, wie z. B. der Cerchar-Abrasivitäts-Versuch zwar notwendig und hilfreich, jedoch nicht hinreichend.

Auch dann, wenn diese Versuche ein gering abrasives Gestein ausweisen, können beim Vortrieb erhebliche Verschleißerscheinungen auftreten. Nur beispielhaft genannt seien die folgenden Effekte:

Schmirgel-Effekt bei Wasserzutritt beispielsweise beim Vortrieb in quarzhaltigen Sandsteinen mit tonigen Bindemitteln

Einseitiges Abschleifen von aufgrund von Verklebung nicht rotierenden Disken in Tonsteinen (siehe hierzu auch Kap. 3.3)

Verschleiß in Wechsellagen aus Ton-/Sandsteinen oder in mixed-face-conditions mit Störungen. 

Entsprechende Überlegungen müssen rechtzeitig angestellt werden, damit die Tunnelvortriebsmaschine und der Vortrieb entsprechend ausgelegt werden. 

3.2 Blocky Ground

In Abhängigkeit von der Raumstellung, dem Abstand und der Ausbildung der Trennflächen kann es in klüftigem Fels zur Ausbildung von Gesteinsblöcken an der Ortsbrust kommen. In diesen Fällen wird der Fels nicht wie gedacht an der Ortsbrust zu Gesteinsstücken (Chips) zermahlen. Vielmehr werden die Gesteinsblöcke von dem Bohrkopf aus dem Verband gerissen und bewegen sich dann unkontrolliert vor dem Bohrkopf, der in einem solchen Fall wie ein Steinbrecher fungieren muss. Die Felsblöcke können erhebliche Schäden an den Abbauwerkzeugen und am Bohrkopf selber sowie auch am nachgelagerten Transportsystem verursachen. Dieses als „blocky ground“ bezeichnete Phänomen ist schon bei einigen Vortrieben im Fels aufgetreten. Beispielhaft genannt seien der Hallandsås-Tunnel in Schweden [5] sowie der Neue Schlüchterner Tunnel [8]. Sind solche Verhältnisse zu erwarten, so müssen die Öffnungen im Bohrkopf, z. B. durch sogenannte grill bars (Stahlstreben), so verkleinert werden, dass die Größe der Gesteinsblöcke, die in das nachgelagerte Transportsystem gelangen, auf ein zulässiges Maß beschränkt wird. Gleichzeitig müssen der Bohrkopf und die Abbauwerkzeuge entsprechend ausgelegt werden (Verstärkung, Verschleißschutz, Möglichkeit des einfachen und schnellen Werkzeugwechsels), und Werkzeugwechsel müssen in Planung und Kalkulation berücksichtig werden. 

3.3 Verklebung

Sedimentgesteine treten häufig als Wechselfolge von gering durchlässigen Ton- oder Schluffsteinen und höher durchlässigen Sand- oder Kalksandsteinen auf (vgl. z. B. typische Schichtfolgen der Formationen des Keupers, Juras, Buntsandsteins). Bei den Tonsteinen handelt es sich häufig um veränderlich feste Gesteine. Bei Austrocknung und anschließender Wasserzufuhr zerfallen sie zu Ton. Dies kann an oberflächigen Aufschlüssen, die der Witterung ausgesetzt sind, beobachtet werden.

Bei TVM-Vortrieben in solchen Formationen, insbesondere unter dem Grundwasserspiegel, ist es wiederholt zu starken Verklebungserscheinungen gekommen. Derartige Beobachtungen wurden beispielsweise beim Vortrieb des Fildertunnels (Stuttgart 21) in den Wechsellagerungen aus Tonsteinen und wasserdurchlässigen Sandsteinen des Stubensandstein unterhalb des Grundwasserspiegels gemacht [15]. Auch beim Vortrieb des Neuen Schlüchternen Tunnels in den Wechsellagerungen aus Ton- und Sandsteinen des Oberen Buntsandsteins wurden derartige Erscheinungen beobachtet [8]. Durch die Verklebungen blockieren die Abbauwerkzeuge, und es kommt zu einseitigem Verschleiß. In der Folge werden in großem Umfang Meißelwechsel erforderlich (Bild 16, [15]). Weiterhin kommt es zu einer deutlichen Abnahme der Vortriebsleistung. Die Verklebung in Kombination mit den höheren Gesteinsfestigkeit der Sandsteinlagen führen zu einem Anstieg der erforderlichen Andruckkräfte und Drehmomente. Die Temperaturen am Bohrkopf nehmen zu.

16| Verklebung in Tonsteinen, Werkzeugverschleiß – Beispiele
Credit/Quelle: WBI (links), Arge ATCOST 21 (rechts)

Im Zusammenhang mit dem Fildertunnel wurden umfangreiche Untersuchungen zu diesem Thema angestellt [15]. Mit Laborversuchen konnte gezeigt werden, das zerkleinerte Tonsteinproben nach Trocknung und anschließender Zufuhr von Wasser zu mittelplastischen Tonen zerfallen, die hinsichtlich ihrer Plastizität und Konsistenz genau in den Bereich stark verklebungsanfälliger Böden nach [16] fallen. Beim TVM-Vortrieb werden die Tonsteine zunächst zerkleinert. Sie sind erhöhten Temperaturen ausgesetzt (s. o.) und können insofern austrocknen. Wasser kann einerseits durch die Sandsteinlagen zufließen. Andererseits wird im Zuge der Konditionierung und der Reinigung Wasser zugeführt. Darüber hinaus werden die Tonsteine beim Vortrieb „mechanisch bearbeitet“. Es liegt also nahe, dass diese veränderlich festen Gesteine aufgrund der Randbedingungen beim Vortrieb zerfallen und in der Folge Verklebungserscheinungen auftreten.

Die Zerkleinerung, mechanische Bearbeitung und die erhöhten Temperaturen sind Einflussfaktoren, die nicht geändert werden können. Als Gegenmaßnahme kommt damit nur die Minimierung der Wasserzufuhr in Frage. Zum einen sollte die Wasserzufuhr aus baubetrieblichen Gründen minimiert werden und etwaige zugeführte Wässer (Reinigung) sollten umgehend abgeführt werden. Der Wasserzufluss aus dem Baugrund (Sandsteinlagen) kann durch eine (ergänzende Beaufschlagung) mit Druckluft minimiert bzw. unterbunden werden. Ein erfolgreiches Beispiel hierfür ist der Vortrieb des Fildertunnels in den Abschnitten im Lias α, ebenfalls unterhalb des Grundwasserspiegels, der ohne Verbreiung unter Druckluft durchgeführt wurde, und bei dem keine Probleme mit Verklebung aufgetreten sind [15].

Zukünftige maschinelle Tunnelvortriebe in Formationen mit veränderlich festen Gesteinen erfordern entsprechende Betrachtungen und weitergehende Untersuchungen, um die Probleme der Verklebung besser in den Griff zu bekommen. 

4 Zusammenfassung

Bei maschinellen Vortrieben liegt ein komplexes Wechelspiel zwischen Tunnelvortriebsmaschine, Baugrund und Tübbingauskleidung vor. Insbesondere für Vortriebe im klüftigen Fels müssen diese Wechselwirkungen in Planung und Bau berücksichtigt werden, da sonst erhebliche Probleme auftreten können, die zu Bauzeit- und Baukosten-Überschreitungen führen.

Eine wesentliche Voraussetzung hierfür ist das Verständnis sowie die realitätsnahe Beschreibung und Erfassung des Spannungs- und Verformungsverhaltens sowie der Durchlässigkeit des Felses, insbesondere der häufig vorliegenden Anisotropien der Festigkeit und Durchlässigkeit. Ein hierfür geeignetes Modell ist das Anisotropic Jointed Rock Model (AJRM).

Im vorliegenden Artikel wird zunächst das Zusammenwirken des Gesamtsystems aus TVM, Baugrund und Tübbingauskleidung dem Grunde nach erläutert. Basierend auf dem Beispiel eines Buntsandsteins wird die realitätsnahe Beschreibung des Felses basierend auf dem AJRM beschrieben. Anschließend werden ausgewählte Ergebnisse von FE-Berechnungen vorgestellt, die an dem o. g. Gesamtsystem unter Berücksichtigung der Wechselwirkungen durchgeführt wurden. Es wird gezeigt, dass das Trennflächengefüge, die Anisotropie der Festigkeit und Durchlässigkeit und die Sickerströmung erheblichen Einfluss auf die Standsicherheit der Ortsbrust, auf die Belastungen und Verformungen im Schild- und Tübbingbereich sowie auch auf die Eignung der Ortsbrust als Widerlager haben. Es ergeben sich daraus wesentliche Bedingungen für die Auslegung der Tunnelvortriebsmaschine (z. B. Pressenkräfte, Bemessung Schild, Bemessung Tübbinge, Erfordernis Druckluftstützung, etc.). Werden die maßgeblichen Eigenschaften des Felses nicht richtig berücksichtigt und wird die Wechselwirkung von Baugrund, Tunnelvortriebsmaschine und Tübbingauskleidung nicht angemessen erfasst, so besteht das Risiko, dass die TVM und die Tübbingauskleidung nicht angemessen geplant werden und beim Vortrieb Probleme auftreten.

Darüber hinaus liegen beim maschinellen Vortrieb im klüftigen Fels besondere Bedingungen hinsichtlich der Ringspaltverfüllung sowie hinsichtlich des Lösens (Verschleiß, Blocky Ground, Verklebung) vor, die entsprechende Maßnahmen erfordern. Auch hierauf wird im vorliegenden Artikel eingegangen.

In der Vergangenheit sind bei maschinellen Vortrieben im klüftigen Fels des Öfteren Schwierigkeiten aufgetreten, die zu einer Überschreitung der vorgesehenen Bauzeiten und -kosten geführt haben. Im Zuge der von der DB Netz AG geplanten Neubaustrecken sind eine Reihe langer Tunnel im klüftigen Fels geplant, die aufgrund ihrer Länge für den maschinellen Tunnelvortrieb in Frage kommen. Die Autoren möchten mit dem vorliegenden Artikel die relevanten Fragestellungen aufzeigen und damit einen Beitrag zu einer besseren Kosten- und Terminsicherheit zukünftiger Projekte leisten.