Baugrundvereisung im durchströmten Untergrund

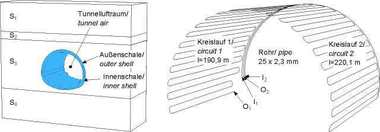
Die künstliche Baugrund-vereisung zur Herstellung statisch tragender und wasserdichter Frostkörper hat sich als begleitende Bauhilfsmaßnahme im Tunnelbau bereits vielfach bewährt und gewinnt gerade in jüngerer Zeit zunehmende Beachtung bei einer Vielzahl aktueller Bauvorhaben. Insbesondere das Auffahren von Querschlägen für Fluchtwege zwischen benachbarten Tunnelröhren (Bild 1) und die Herstellung unterirdischer Haltestellen durch die bergmännische Aufweitung im Nachgang zu maschinell vorgetriebenen Streckentunneln stellen interessante, aktuelle und zukunftsträchtige Aufgabengebiete für das Gefrierverfahren im Tunnelbau dar [8, 10]. Neben den rein technischen Vorzügen durch das breite Einsatzspektrum in den unterschiedlichsten Bodenarten hebt sich das Verfahren auch im Hinblick auf seine Umweltverträglichkeit von anderen Verfahren positiv ab, da es reversibel durchführbar ist und keine nachteiligen Rückstände im Boden bzw. Grundwasser verbleiben. Oft scheitert der planmäßige Einsatz jedoch an den hohen Energiekosten für den Wärmeentzug aus dem Boden. Neben dem reinen Gefriervorgang  können sich diese noch zusätzlich erhöhen, wenn weitere thermische Einflüsse durch Zusatzinstallationen und erhöhten Energieeintrag der Gefrieranlage kompensiert werden müssen (Bild 2).
Eine zuverlässige Ermittlung der benötigten Zeit zum Aufgefrieren der vorgesehenen Frostkubatur muss die Wärmemengen, die das Temperaturregime im Boden bestimmen und den Gefrierfortschritt maßgeblich beeinträchtigen können, berücksichtigen. Im Vergleich zu anderen thermischen Einflüssen einer oberflächennahen Vereisungsmaßnahme (Bild 2) lässt sich dabei eine Grundwasserströmung als gefrierzeit- und kostenbestimmend charakterisieren [2].
Selbst bei vermeintlich moderaten Grundwasserfließgeschwindigkeiten ist der konvektive Wärmeeintrag aufgrund der hohen Wärmekapazität des Wassers beachtlich: Eine Grundwasserströmung, die eine Temperatur von 13  °C besitzt und mit 1,0  m/d (Filtergeschwindigkeit) fließt, erzeugt eine Wärmestromdichte von ca. 630  W/m2. Dies entspricht in etwa der Wärmestromdichte der Sonne auf der Erdoberfläche an einem klaren, sonnigen Früh-lingstag auf Sylt (600  W/m2). Die Spitzenwerte der mittäglichen Solarstrahlung liegen in Deutschland im Sommer bei ca. 900  W/m2. Dieser Wärmeeintrag wird bereits durch eine Grundwasserströmung von 1,5  m/d erreicht. Im stark durchströmten Untergrund kann das Frostwachstum folglich gänzlich zum Erliegen kommen, wenn sich ein thermisches Gleichgewicht zwischen der herantransportierten und der durch die Gefrierrohre entzogenen Wärmemenge einstellt. Der Frostkörper kann dann seine angedachte Funktion nicht übernehmen. Hohe Strömunggeschwindigkeiten über das Maß der natürlichen Strömung hinaus können insbesondere im Bereich vorhandener Bebauung als Folge von Düseneffekten oder in zwischengelagerten Grobschichten mit hohen Durchlässigkeiten auftreten.

1 Wärmeübertragung und Wassertransport im Boden
1.1 Physikalische Grundlagen
Der vorherrschende Wärmeübertragungsmechanismus in Böden ist die reine Wärmeleitung [5]. Die Ursache dieses Energietransports liegt in einem Temperaturgefälle und erfolgt durch atomare Wechselwirkung zwischen benachbarten Molekülen. Der entstehende Wärmestrom Q [J/s bzw. W] ist dabei dem Temperaturgefälle und der betrachteten Querschnittsfläche proportional. Der Proportionalitätsfaktor ist eine stoffspezifische, meist temperaturabhängige Größe und wird als Wärmeleitfähigkeit  [W/(mK)] bezeichnet (Gesetz nach Fourier). Andere Mechanismen wie beispielsweise die Wärmestrah-lung spielen bei hohem Sättigungsgrad im ruhenden Grundwasser keine entscheidende Rolle.
Bei strömendem Grundwasser muss zusätzlich der Effekt der erzwungenen Konvektion berücksichtigt werden. Diese beschreibt einen Wärmetransport durch Grundwasserströmung, die durch Potenzialunter-schiede oder Pumpvorgänge hervorgerufen wird. Die infolge einer Wasserströmung transportierte Wärmemenge hängt wesentlich von deren Temperatur und Filtergeschwindigkeit vf ab.
Die Filtergeschwindigkeit vf des konvektiven Terms ergibt sich aus dem weithin bekannten Gesetz von Darcy:

    h
vf = kf ·        kf · i
    l
Demnach ist die Strömungsgeschwindigkeit des Wassers proportional zum hydraulischen Gefälle i (Bild 3). Der Durchlässigkeitsbeiwert kf [m/s] ist von den Strömungseigenschaften des Fluides und den Eigenschaf-ten des durchströmten Mediums abhängig [6]. Da die Fluideigenschaften Dichte und Vis-kosität temperaturabhängig sind, ist auch der kf-Wert in dem für eine Baugrundvereisung relevanten Temperaturspektrum keinesfalls konstant. Selbst im ungefrorenen Zustand schwankt seine Größe so stark mit der Temperatur, dass diese Veränderung für eine zuverlässige Erfassung der Strömung nicht vernachlässigt werden darf.
Das Temperaturfeld beeinflusst somit durch die Temperaturabhängigkeit der Wasser-eigenschaften den Durchlässigkeitsbeiwert und damit die Filtergeschwindigkeit, die wiederum in den Konvektionsterm der Wärmetransportgleichung eingeht. Es liegt somit ein vollständig gekoppeltes Problem vor. Bild 4 zeigt schematisch den Modellzusammenhang.

1.2 Temperaturabhängigkeit der Bodenkennwerte
Die Temperaturabhängigkeit der thermischen und hydraulischen Kenngrößen muss bei der Berechnung von Vereisungsmaßnahmen berücksichtigt werden. Diese begründet sich zum einen in den temperatur-abhängigen Eigenschaften der einzelnen Bodenbestandteile Feststoff, Wasser und Eis selbst, insbesondere aber in ihrer veränderlichen mengenmäßigen Zusammensetzung im Laufe des Gefrierens.
Bild 5 zeigt beispielhaft den qualitativen Verlauf der thermischen Kennwerte Wärmeleit-fähigkeit   (T) und Wärmekapazität c  (T) eines Bodens unter Berücksichtigung des Phasenwechsels des Porenwas-sers während des Gefrierens. Besonders auffällig ist der Anstieg der Wärmekapazität im Gefrierintervall zwischen Solidus- (Ts) und Liquidustemperatur (TL) zu erkennen, der aus der Freisetzung der latenten Wärme L resultiert. Diese beträgt für reines Wasser L = 333 600 J/kg und würde damit immerhin ausreichen, um die Temperatur von 1 kg Wasser (cs,w = 4200 J/kgK) um knapp 80  °C zu erhöhen. Die freigesetzte Wärme verzögert den Gefrierprozess und hat dadurch einen deutlichen Einfluss auf den Frostfortschritt. Beim Schmelzvorgang muss diese Energiemenge hingegen aufgebracht werden, um die Kristallstruktur des Eises aufzubrechen. Erst dann ändert sich die Temperatur des gefrorenen Bodens wieder. In dieser Tatsache begründet sich die Trägheit von gefrorenem Boden beim Auftauvorgang, die einen nicht zu unterschätzenden Sicher-heitsaspekt bei kurzfristigen Funktionsstörungen des Ge-friersystems einer Baumaßnah-me bietet. Ein schlagartiges Auftauen findet nicht statt.
Die Anforderungen an ein Lösungsmodell zur Beschrei-bung der Frostausbreitung bei Berücksichtigung einer Grundwasserströmung ergeben sich aus den vorgenannten Zusam-menhängen. Es sind demnach zeitabhängige (instationäre), nichtlineare (die thermischen und hydraulischen Kennwerte sind abhängig von der Temperatur) und vollständig gekoppelte Wärmetransport-Grund-wasserströmungsberechnungen durchzuführen. Dazu werden numerische Verfahren erforderlich.
Die im Folgenden vorgestellten Ergebnisse von Gefrierbe-rechnungen beruhen auf einem vereinfachten, praxistauglichen Phasenwechselmodell, welches für die Gefrierzeitprognose im Tunnelbau das thermische und hydraulische Verhalten eines gefrierenden Bodens hinreichend genau beschreibt. Deutlich entscheidender für die Eliminierung von Unsicherheiten bei der Gefrierzeitprognose ist die zutreffende Beschreibung der Strömungsgeschwindigkeit und -richtung des Grundwassers [2].

2 Vereinfachtes Phasenwechselmodell
Die für eine numerische Vereisungssimulation notwendigen Eingangsparameter lassen sich in einer Vielzahl von Fällen auf wenige bekannte Standardgrößen wie Dichte, Kornverteilung etc. reduzieren, die im Rahmen der üblichen geotechnischen Untersuchungen ohnehin bestimmt werden. Die Übertragung geotechnischer Kennwerte auf wärmetechnische Parameter gelingt deshalb, weil sich die thermischen Kennwerte Wärmeleitfähigkeit und Wärmekapazität, die Durchlässigkeit und das Gefrierverhalten eines wassergesättigten, nichtbindigen Bodens hinreichend genau über einfache mathematische/physikalische Modelle aus diesen ableiten lassen [7]. Dazu müssen lediglich die Volumenanteile von Feststoff, Wasser und Eis für jede Temperatur bekannt sein, wenn die Kontinuumstheorie zugrunde gelegt wird [4]. In der veränderlichen Aufteilung des Porenanteils n auf die Eis- und die Wasserphase, ni und nw, im gefrorenen Zustand liegt die Hauptursache für die Tempe-raturabhängigkeit des Boden-verhaltens (Bild 6).
Im Kernpunkt des Lösungs-modells wird die Abnahme des Wassergehalts nw mit Unterschreiten der Gefriertempera-tur durch eine Gefrierfunktion  ausgedrückt, die theoretisch Werte zwischen Null (vollständig gefroren) und Eins (ungefroren) annehmen kann und die Aufteilung mathematisch wie folgt beschreibt:

nw = n ·  mit 0 ≤  ≤ 1

Der zunehmende Eisanteil ergibt sich daraus bei vollständiger Sättigung als Komplementärgröße zu:

ni = n – nw

Der genaue Verlauf der Gefrierfunktion  ist bodenabhängig. Es zeigt sich jedoch, dass die Beschreibung des Verlaufs von  auf Basis des ungefrorenen Wassergehalts wu möglich ist, da auch für Tem-peraturen unterhalb des Ge-frierpunkts nicht alles Wasser gefroren ist. Der aktuelle Wert von wu ist ein direkter Indikator für den Gefrierverlauf und lässt sich mit hinreichender Ge-
nauigkeit über die spezifische Oberfläche aus der Kornverteilung des Bodens ableiten. Spezielle Versuche im Frostlabor erübrigen sich dadurch.
Durch die Implementierung dieses Phasenwechselmodells („Freezing-Modul“) wurde das bestehende Finite-Differenzen-Programm SHEMAT (Simulator for Heat and Mass Transport [3]) für den Anwendungsbereich oberflächennaher Vereisungs-maßnahmen erweitert und zur Ableitung von Optimierungs-empfehlungen einer Querschlagvereisung unter Strö-mungseinfluss herangezogen [2]. Im Folgenden werden einige Erkenntnisse vorgestellt.

3 Einfluss einer Grundwasserströmung
Es wird beispielhaft der Aufgefrierprozess eines kreisrunden, symmetrischen Frost-körpers unter horizontalem Strömungseinfluss in Oberflä-chennähe untersucht. Die gewählten Abmessungen orientieren sich an denen einer typischen Querschlagvereisung. Der lichte Innendurchmesser des Ausbruchprofils soll 5,50  m und die statisch erforderliche Frost-körperdicke 1,50  m betragen. Im so genannten Basissystem, welches als Referenzfall dient, sind 18 Gefrierrohre mit einem gegenseitigen Abstand von ca. 1,22  m gleichmäßig über den Umfang angeordnet. Aus Symmetriegründen braucht nur eine Tunnelhälfte betrachtet zu werden (Bild 7).
Zur Untersuchung des Ein-flusses einer Grundwasserströ-mung auf den Gefrierprozess wird deren Geschwindigkeit in den Simulationen sukzessive erhöht. Dabei wird ein Spektrum von 0,25  m/d bis 1,50  m/d für die Filtergeschwindigkeit abgedeckt. Für größere Filtergeschwindigkeiten kommt das Frostkörperwachstum an kritischen Stellen zum Erliegen, so dass kein vollständiger Frost-körperschluss erzielt werden kann. Die dringende Notwendigkeit, die tatsächlich vorherrschende Grundwassersituation auch schon in der Planungsphase zu erfassen, wird besonders deutlich, wenn die Frostkörpergeometrie zu gleichen Zeit-punkten, aber für unterschiedlich große Strömungsgeschwindigkeiten gegenübergestellt wird. In Bild 8 ist dies für das Basissystem für den Zeitpunkt vorgenommen worden, für den im undurchströmten Fall bereits der gesamte Aufgefriervorgang beendet ist (t = 20 d).
Für das Basissystem hat sich erwartungsgemäß die Luv-Seite unabhängig von der Fließgeschwindigkeit als gefrierzeitbestimmend herausgestellt. In Bild 9 sind die Aufgefrierzeiten über alle untersuchten Fließge-schwindigkeiten aufgetragen. Es zeigt sich, dass die Aufge-frierzeit für das Basissystem bei zunehmender Strömungsgeschwindigkeit erst näherungsweise linear und dann stark exponentiell ansteigt. Die Auftragung lässt auch die kritische Geschwindigkeit erahnen, für die die Gefrierzeit bei diesem Boden gegen Unendlich geht, d. h. der Frostkörper nicht mehr geschlossen werden kann.
Eine unzureichende oder gar fehlende Erkundung der Fließ-geschwindigkeit oder eine nur überschlägige Ermittlung auf Basis eines geschätzten kf-Werts mit Schwankungsbreiten von einer Zehnerpotenz oder mehr kann folglich zu gravierenden Fehleinschätzungen der Gefrier-zeiten führen. Ein Planungs-fehler, der dann mit enormem Aufwand während der Ausführung kompensiert werden muss. So erhöhen sich beispielsweise die Kosten bei einer Fließgeschwindigkeit von 1  m/d im Vergleich zu einer Geschwindigkeit von 0,5  m/d für das hier vorgestellte Beispiel um 46  %. Eine Fehleinschätzung der Strömungsverhältnisse in dieser Größenordnung ist in der Planungsphase bei mangelnder Erkundung leicht vorstellbar.

4 Modifizierte Vereisungskonzepte
Das Ziel von optimierten Entwurfsvarianten muss darin liegen, eine Vergleichmäßigung des Frostfortschritts in den durch die Strömung unterschiedlich stark beanspruchten Bereichen zu erreichen. Dies lässt sich installationsseitig beispielsweise durch die Umpositionierung der geplanten oder die Installation zusätzlicher Gefrierrohre und betriebsseitig durch eine bedarfsgerechte Ansteuerung von Rohrgruppen erzielen [11, 1].
Selbst ohne Installation zusätzlicher Gefrierrohre lässt sich als Folge einer strömungsangepassten Anordnung die Aufgefrierzeit im vorliegenden Beispiel um 20  % reduzieren. Dies kann z.  B. durch Verdich-tung der Gefrierrohre im Luv-bereich oder Ausrücken der Gefrierrohre aus der Mittellinie in den Luvbereich erfolgen.
Eine noch größere Wirkung kann durch eine Vorkühlung des Grundwassers bei Positio-nierung zusätzlicher Rohre im Zustrom erzielt werden. Durch diese Anordnung wirkt sich der Vorkühleffekt besonders stark aus und es wird gleichzeitig ein keilartiger Frostkörper zur Ablenkung der Strömung gebildet (Bild 10). Der Querschlag ist somit auch im Luvbereich nicht mehr frontal der Strömung ausgesetzt. Die dadurch erzielbaren Gefrierzeitverkürzungen sind beachtlich. Durch den Einsatz von insgesamt nur 4 zusätzlichen Gefrierrohren lässt sich so in diesem Fall die Aufgefrierzeit von 50 Tagen im Basissystem auf 25 Tage halbieren. Es entsteht ein sehr gleichmäßiger Frostfortschritt entlang des kompletten Umfangs des Querschlags. Aus thermischen Gesichtspunkten ist die Vorkühlung als sehr effektiv einzustufen. Es muss allerdings geprüft werden, ob eine bau-praktische Umsetzung überhaupt möglich ist.
Da nur ein Teil der Kosten von der Fließgeschwindigkeit abhängt, wirkt sich die Gefrierzeitverkürzung nicht in gleichem Maße auf die Kostenreduktion aus, zeigt aber für das Optimierungsbeispiel mit Vorkühlung trotz zusätzlich installierter Gefrierrohre ein mögliches Einsparpotenzial von gut 20 %.
Die Vereisungssimulationen machen jedoch auch deutlich, dass durch den Eingriff in das Temperaturfeld und veränderte Fließwege der kritische Bereich oft nur verlagert wird, ohne eine Gesamtreduktion der Aufgefrierzeit zu erzielen. Für eine zuverlässige Beurteilung einer Variante ist das System daher stets gesamtheitlich zu betrachten.
Die Vorteile einer bestimmten Entwurfsvariante hängen von der vorhandenen Fließge-schwindigkeit und Fließrichtung ab. Eine pauschale Optimierungsempfehlung für alle denkbaren Fließgeschwindigkeiten und Frostkörpergeometrien ist daher nicht zielführend. Voraussetzung für eine projektspezifische Optimierung ist stets die zuverlässige Erkundung der Strömungsverhältnisse, damit die kritischen Bereiche eines Systems sicher identifiziert werden können. Es muss geprüft werden, ob eine starke Richtungsänderung oder sogar völlige Umkehr der Strömung, beispielsweise durch Hochwassersituationen in Flussnähe, auftreten kann, da sich dadurch die vermeintliche Vorteilhaftig-keit eines Systems schnell zu einem Nachteil für die Gesamtsituation auswirken kann [2].
Aus den bisher am Lehrstuhl für Geotechnik im Bauwesen der RWTH Aachen/D durchgeführten Untersuchungen lassen sich u.  a. die folgenden Empfehlungen für eine Verkürzung der Aufgefrierzeit bzw. Optimierung der Betriebsweise bei einer Vereisungsmaßnahme unter Strömungseinfluss ableiten. Diese können im Planungspro-zess als eine Hilfestellung auf dem Weg zu einem für die Situation optimierten System dienen:
– Die Fließgeschwindigkeit und -richtung ist die maßgebliche Eingangsgröße in den Berechnungen. Mit zunehmender Fließgeschwindigkeit steigt die Aufgefrierzeit exponentiell an.
– Die Fließgeschwindigkeit kann am zuverlässigsten aus Pegelmessungen abgeleitet werden, wenn die Durchlässigkeit bekannt ist. Diese sollte vorzugsweise mittels Pumpversuch bestimmt werden. Mögliche Änderungen der Größe oder Richtung der Strömung im Laufe der Baumaßnahme sollten zwingend in der Planungsphase Berücksichtigung finden.
– Für eine zielführende Optimierung muss vorab der gefrierzeitbestimmende, kritische Bereich für die vorliegende Strömungssituation lokalisiert werden. Bei äquidistanter Rohranordnung ist dies in der Regel der Luvbereich.
– Eine Verdichtung des Rohrab-standes im Luvbereich ist der Verdichtung im Leebereich zur Erzielung einer kürzeren Schließzeit vorzuziehen. Im Leebereich ist nicht so sehr der Abstand der Rohre, sondern in großem Maße auch die Abschirm- und Vorkühlwirkung aus dem Luvbereich für die Schließzeit relevant.
– Es sollte stets nachvollzogen werden, inwieweit sich ein Frostkörperschluss im Luvbe-reich durch eine Fließwegverlagerung nachteilig auf den Übergangsbereich zum First auswirkt. Bildet sich ein neuer kritischer Bereich mit einer Durchströmungsmöglichkeit, so ist die vorgesehene Gefrierzeit-verkürzung gefährdet. Günstig ist eine frühzeitige Ablenkung der Strömung über den First.
– Die Vorkühlung des Grundwassers erweist sich als sehr effektive Maßnahme, um die Aufgefrierzeit zu verkürzen. Es sollte daher geprüft werden, inwieweit sich Gefrierrohre im Zustrom des Grundwassers so platzieren lassen, dass sie nach dem Aufbau des Frostkörpers zusätzlich eine Ablenkung der Strömung herbeiführen.
– Die intermittierende Betriebsweise lässt sich optimieren, wenn die Rohre zu einzelnen Gruppen gebündelt werden, damit sie bedarfsgerecht angesteuert werden können. Insbe-sondere im Leebereich bietet sich großes Einsparpotenzial durch zeitweise Unterbrechung des Gefrierbetriebs.
Abschließend sei der Wayss & Freytag Ingenieurbau AG seitens der Autoren für die finanzielle Unterstützung und die Bereitstellung von Baustellendaten im Rahmen des durchgeführten Forschungsvorhabens am Lehrstuhl für Geotechnik im Bauwesen der RWTH Aachen gedankt. Ebenso gedankt sei der Entwicklergruppe von SHEMAT um Professor Clauser für ihre tatkräftige Unterstützung.

Literatur
[1] Baier, Ch., Ziegler, M., Mottaghy D., Rath V. (2008): Numerische Simu-lation des Gefrierprozesses bei der Baugrundvereisung im durchströmten Untergrund. Bauingenieur 83 (2008), H. 2, S. 49–60.
[2] Baier, Ch. (2008): Thermisch-hydraulische Simulationen zur Optimierung von Vereisungsmaßnahmen im Tunnelbau unter Einfluss einer Grundwasserströmung. Dissertation am Lehr-stuhl für Geotechnik im Bauwesen der RWTH Aachen (Mitteilungsheft im Druck).
[3] Clauser, C. (2003): Numerical Simulation of Reactive Flow in Hot Aquifers – SHEMAT and Processing SHEMAT, Springer-Verlag Berlin Heidelberg.
[4] de Boer, R.; Bluhm, J.; Wähling, M.; Ricken, T. (2003): Phasenübergänge in porösen Medien, Forschungsbericht aus dem Fachbereich Bauwesen 98, Universität Duisburg-Essen.
[5] Farouki, O.T. (1986): Thermal Properties of Soils. Trans Tech Publications, Series on Rock and Soil Mechanics, Vol. 11.
[6] Hubbert, M.K. (1956): Darcy’s law and the field equations of the flow of underground fluids, Transactions of the American Institute of Mining, Metallurgical and Petroleum Engineers, Vol. 207, pp. 222–239.
[7] Johansen, O.; Frivik, P.E. (1980): Thermal properties of soils and rock materials; Proceedings of the 2nd International Symposium on Ground Freezing, NTH, Trondheim, Norwegen.
[8] Müller, B.; Orth, W. (2005): Bodenvereisung unter schwierigen Bedingungen: Bahnsteigerweiterung beim U-Bahnhof Marienplatz München, STUVA Forschung und Praxis, 41,
S. 111–115.
[9] Orth, W. (1986): Gefrorener Sand als Werkstoff. Veröffentlichungen des Institutes für Bodenmechanik und Felsmechanik der Universität Frideri-ciana in Karlsruhe, Heft 100.
[10] Weigl, H.; Dausch, G. (2006): Bodenstabilisierung durch Stickstoff- und Solevereisung anhand ausgeführter Beispiele in Deutschland und in den Niederlanden. Beiträge zum 21. Christian Veder Kolloquium. Hrsg.: M. Dietzel, W. Schubert, H. F. Schweiger; S. Semprich., S. 179–194.
[11] Ziegler, M., Baier, Ch. (2007): Optimierung von Vereisungsmaßnah-men im Tunnelbau durch Anwendung numerischer Simulationen. Tunnel verbinden – Connections by Tunnels: Vorträge der STUVA-Tagung 2007 in Köln/Hrsg.: Studiengesellschaft für unterirdische Verkehrsanlagen STUVA. Gütersloh: Bauverlag, 2007. S. 177–183. (Forschung + Praxis 42).