Herausforderungen an das Tübbingdesign bei einem Tunneldurchmesser über 19 m

1 Einleitung

Tübbingringe zur Auskleidung von maschinell vorgetriebene Tunneln sind Stahlbetonfertigteile und bei der Konstruktion sowie Bemessung als solche zu behandeln. Da im Tunnelbau aber gewisse Besonderheiten zu berücksichtigen sind, stellt das Design von Tübbingringen Anforderungen, die ganz erheblich von denen an sonstige Stahlbetonkonstruktionen abweichen. Vor allem die Festlegung der Einwirkungen im Bau- und Endzustand und die Bettung des Gelenkringes im umgebenden Boden müssen aus den Baugrundkennwerten richtig erkannt und auf das Ringmodell angesetzt werden.

Bei den im Kanal- und U-Bahnbau üblichen Durchmessern von weniger als 7 m und den meist moderaten Überdeckungen können Vorgaben gemacht werden, die auf der „sicheren Seite“ liegen. Bei größeren Durchmessern, beispielsweise für Hochgeschwindigkeits-Bahntunnel oder für mehrspurige Straßentunnel, müssen realistischere Kennwerte in die Konstruktion und die Statik eingeführt werden. Anderenfalls kann es sein, dass der Ring nicht zu bemessen ist oder unwirtschaftliche Abmessungen aus den Berechnungen ermittelt werden. Dazu kommen neuerdings die Schwierigkeiten bei der Bemessung für den Brandfall.

Der bisher größte ausgeführte, maschinell aufgefahrene und mit Tübbingen ausgekleidete Tunnel ist der Jangtse River Tunnel in Shanghai/China mit einem Ausbruchdurchmesser von 15,40 m. Momentan wird in Italien ein noch etwas größerer Autobahntunnel mit 15,50 m Ausbruchdurchmesser hergestellt (Autobahn A1, Bologna-Florenz/Italien, Galleria Sparvo). Beim größten in Planung befindlichen, maschinell aufgefahrenen Tunnel (Neva-Autobahnunterquerung, Orlovski-Tunnel in St. Petersburg/Russland) wird der Ausbruchdurchmesser ca. 19,20 m betragen. Dies entspricht der Höhe eines sechsstöckigen Gebäudes. Die Ortsbrustfläche beträgt 284 m² (Bild 1).

2 Projektbeschreibung

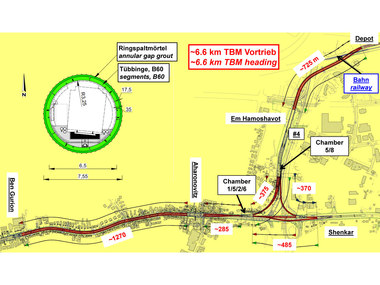
Die Neva durchquert St. Petersburg, die zweitgrößte Stadt Russlands mit ca. 5 Mio. Einwohnern, von der Ostsee kommend bis zu den Hafenanlagen im Osten der Stadt und den Ladogasee. Alle Brücken über die Neva werden zu regelmäßigen Zeiten - hauptsächlich nachts – mehrere Stunden geöffnet, um auch großen Schiffen die Durchfahrt zu den Hafenanlagen zu ermöglichen (Bild 2). In diesen Öffnungszeiten kann die Neva bisher nicht überquert werden.

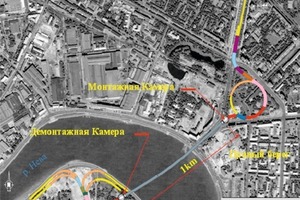
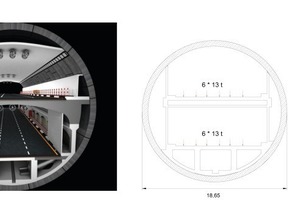
Der geplante „Orlovski-Tunnel“ würde die Verkehrssituation erheblich verbessern und die nachts getrennten Stadthälften verbinden. Nach der Fertigstellung könnten Fahrzeuge rund um die Uhr von einem Ufer der Neva ans andere gelangen (Bild 3). Die Brücken könnten für den ständig anwachsenden Schiffsverkehr länger als bisher geöffnet bleiben. Der Tunnel soll als PPP-Projekt (Public-Private-Partnership) hergestellt werden. Die Baukosten werden auf ca. 1,4 Mrd. Euro geschätzt und sollen sich über Mauteinnahmen rückfinanzieren.

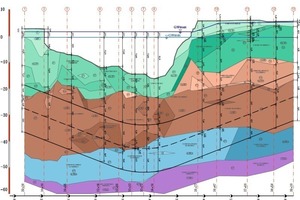
Die Geologie im Bereich der Neva-Unterquerung ist geprägt durch quartäre Sedimente die hauptsächlich durch Flussablagerung beim Abschmelzen der eiszeitlichen Gletscher entstanden sind. Durch mehrmaliges Wiedervordringen der Vergletscherung wurden die Böden stark belastet und sind dadurch meist überkonsolidiert. Im geo-
logischen Längsschnitt (Bild 4) sind die unterschiedlichen Schichten dargestellt. Die Bodenkennwerte sind über die ganze Tunnelhöhe und darüber als sehr schlecht zu bezeichnen. Die tonig, schluffigen Feinsande haben überwiegend eine Wichte von γ ≈20 kN/m³, einen E-Modul von E ≈ 10 bis 30 MN/m², eine Querdehnzahl ν ≈ 0,3 bis 0,4, ein φ ≈ 20° und eine Kohäsion c ≈ 15 kN/m².

3 Lastannahmen /
Bettung

Bei der Tiefenlage des Tunnels im Bereich von weniger als 2 Durchmessern wird auf die volle Bodenauflast bemessen. Eine Reduzierung der vertikalen Lasten aufgrund der Silowirkung nach Terzaghi wird für den Endzustand meist nicht zugelassen. Bei ca. 22 m Überdeckung ergaben sich beim Orlovski-Tunnel maximale Auflasten von ca. 440 kN/m².

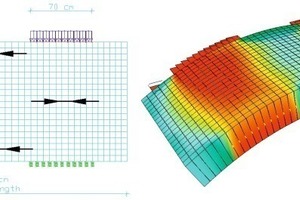
Berechnungen nach der Methode der Finiten Elemente zeigen, dass eine Reduzierung der Lasten um ca. 25 % durchaus möglich wäre. Dies entspricht in etwa der Terzaghi-Abmin-
derung und wurde bei der Bemessung auch genutzt. Die volle Auflast wurde zusätzlich als Lastfall mit reduzierten Sicherheiten nachgewiesen.

Die horizontale Einwirkung auf den Ring wird über den Seitendruckbeiwert festgelegt. Beim Orlovski-Tunnel konnte der k₀-Wert nur über den Winkel der inneren Reibung bestimmt werden (k₀= 1 - sin φ‘).
In den relevanten Schichten im Bereich des Tunnels ergaben sich hieraus Seitendruckbeiwerte zwischen 0,6 und 0,75. Aufgrund der möglichen Überkonsolidierung der Böden wurde auch mit einem Seitendruckbeiwert von 1,0 gerechnet. Höhere Seitendrücke, resultierend aus der Überkonsolidierung der Böden, müssen nicht gerechnet werden. Bei Seitendrücken über k₀=1,0 bauen sich diese bereits bei geringsten Verformungen sofort auf Werte unter 1 ab. Aus der Berechnung ergab sich, dass bereits geringe Variationen des Seitendruckbeiwertes zu großen Unterschieden in den daraus resultierenden Biegemomenten führten.

Üblicherweise wird für die Berechnung des Tübbingringes mit der Methode der Finiten Elemente (FEM) eine zweidimensionale Scheibe berechnet. Auf Grund der Vereinfachungen der zweidimensionalen Scheibenberechnung wird die Last-
umlagerung vom primären zum sekundären Spannungszustand nach dem Stützkern- oder Stützlastverfahren durchgeführt. Die Lastumlagerung an der Ortsbrust kann durch eine Abminderung der Steifigkeit des stützenden Kerns oder durch reduzierte Spannungen auf den Restquerschnitt simuliert werden. Zwischen Setzungsberechnung bzw. Lastumlagerungsberechnung und Tunnelbemessung muss dabei unterschieden werden. Um realistische Setzungsbeträge/ Lastumlagerungswerte zu berechnen, müssen Faktoren, wie vorauseilende Umlagerung in Tunnellängsrichtung, Auflockerung der Ortsbrust und Überschnitt der Maschine berücksichtigt werden.

Da hohe zugelassene Verformungen umfangreiche Spannungsumlagerungen im Boden verursachen, sind die verbleibenden Beanspruchungen des Tunnels gering. Beim Einsatz einer TVM mit Ortsbruststützung wird die Entspannung jedoch relativ gering ausfallen. Nach der Schilddurchfahrt wird der Boden aber durch die Ring-
spaltverpressung wieder vorgespannt. Mit der Aushärtung des Verpressmörtels stellen sich wieder höhere Spannungen und damit Lasteinwirkungen auf den Tübbingring ein. Um dies rechnerisch nachzuvollziehen sollten die Entspannungserscheinungen an der Ortsbrust nur mit geringen Abminderungen der Steifigkeiten bzw. Kernspannungen in die Berechnung eingeführt werden.

Aufgrund der großen Unsicherheit bei der Festlegung der Kennwerte sowie möglicher Streuungen der Eingangsgrößen waren umfangreiche Parameterstudien erforderlich. Dadurch wurde die Bandbreite der Einwirkungen erfasst und das Verständnis für die spezifische Baugrund-Bauwerk-Interaktion erarbeitet.

Im Gegensatz zum Spritzbeton und Ortbeton unterliegt der Tübbingring bereits bei der Herstellung, dem Transport und der Montage erheblichen Belastungen. Er wird bereits im sehr jungen Zustand aus der Schalung gehoben und bewegt.

Für die geometrische Ausbildung und die Bemessung des Tübbingringes mit maßgebend sind die Einwirkungen aus dem Maschinenvorschub. Beim vorgesehenen Vortriebsschild mit flüssigkeitsgestützter Ortsbrust und einem Außendurchmesser von 19,2 m wirken 37 Doppelpressen mit bis zu 7000 kN auf eine begrenzte Fläche in der Ringfuge. Hier entstehen hohe Druckkräfte. Insbesondere die dadurch geweckten Spaltzugkräfte in Längs- und Querrichtung können maßgeblich für die Bewehrung und die Ringdicke werden (Bild 5).

Die Erfassung der Einwirkungen aus Zwängungen im Schildschwanz ist nur schwer vorauszusagen und nachzuweisen. Die Verwendung eines ausreichend konischen Ringes (konisch auf der schildabgewandten Seite!) und einer Schwanzluft von mindestens 4 cm sollten unzulässige Belastungen jedoch vermeiden.

Bei üblichen Verkehrstunneln kann auf den Ansatz von inneren Lasten meist verzichtet werden. Der mehrstöckige Orlovski-Tunnel weist jedoch hohe Verkehrslasten auf, die mittels umfangreicher Einbauten die Lasten konzentriert in den Tübbingring einleiten. Da in den weichen Böden mit geringen Steifemoduli Verformungen möglich sind, mussten die inneren Lasten gesondert ermittelt und in der Statik weiter verfolgt werden (Bild 6).

4 Bettungsannahmen

Aufgrund der Längsfugen im Tübbingring, die als Gelenke wirken, muss eine ausreichende Bettung die Stabilität des Ringes gewährleisten. Die Bettung errechnet sich aus dem Verformungs- bzw. Elastizitätsmodul des umgebenden Gebirges. Auch wenn die modernen Rechenprogramme, insbesondere diejenigen die nach der Methode der Finiten Elemente arbeiten, eine Vielzahl von Modellen zur Verfügung stellen, ist die Ermittlung der Kennwerte schwierig.

Vom Baugrundgutachter wird meist der E-Modul (Youngs‘ Modulus) vorgegeben. Aus dem E-Modul wird zur Ermittlung der Federsteifigkeiten der Bettungsfedern mit der Querdehnzahl ν in den Steifemodul E_S umgerechnet.

Insbesondere in den weichen Schluff- und Tonböden ergibt sich eine deutliche Erhöhung des Steifemoduls gegenüber dem E-Modul des Bodens (Tabelle 1).

Aus dem Steifemodul errechnet sich die Bettungsfederkonstante (für Stabzugberechnungen) mit der Formel (R = Radius der Tübbingringsystemlinie):

Die Baugrundgutachter neigen dazu, geringe Verformungs- und E-Module vorzugeben, um auch „Ausreißer nach Unten“ zu erfassen. Dabei wird häufig übersehen, dass sich dünnere weiche Bodenschichten nicht wirklich auf die Bettungsverhältnisse auswirken. Zudem erzeugt der Stützdruck an der Ortsbrust und der Verpressdruck des Ringspaltmörtels eine Vorspannung des Baugrundes, der im kritischen Bereich nahe der Vortriebsmaschine zu einer weiteren Vergleichmäßigung der Bettungsverhältnisse sorgt.

Die Bestimmung der Entlastungs- und Wiederbelastungsmodule, die bei der Ermittlung der Bettungsfederkonstante anzusetzen sind, bereitet häufig größere Schwierigkeiten. Sie kann aus Triaxialversuchen oder auch Oedometerversuchen ermittelt werden, wird aber meist nur abgeschätzt.

Bei großen Ringdurchmessern mit geringer Überdeckung muss beachtet werden, dass der Ring sich rechnerisch zu einem „stehenden Ei“ verformen kann. Dabei wird auch in der Firste eine Bettung geweckt, die bei den üblichen Ringberechnungen nicht auftritt, und deren Verträglichkeit stets zu überprüfen ist. Gerade bei internationalen Großprojekten ist es angebracht, die Verformungsmodule genau zu hinterfragen und mit den Baugrundingenieuren zu diskutieren.

So wäre der Orlovski-Tunnel mit den ursprünglich vorgegebenen Parametern nicht ausführbar gewesen. Nach ausführlichen Diskussionen konnten jedoch realistische Kennwerte im Einvernehmen festgelegt werden, mit denen der Tübbing-ring zu bemessen war.

5 Ringkonstruktion

Als erster Schritt bei der Konstruktion wird die Ringteilung festgelegt. Wenige Segmente pro Ring ergeben eine größere Steifigkeit, geringere Verformungen aber auch höhere Biegemomente in den Einzelsegmenten. Mehr Segmente pro Ring ergeben entsprechend größere Verformungen und geringere Biegemomente.

Durch eine Vergleichsberechnung wurde der Einfluss der Anzahl der Tübbinge pro Ring ermittelt. Die Ergebnisse zeigen, dass sich bei einer Ringteilung 9 + 1 gegenüber dem Ring mit der Teilung 12 + 1 die Biegemomente um ca. 20 % erhöhen, die Verformung aber um ca. 10 % geringer sind. Durch die stärkere Verdrehung in den Längsfugen und die dadurch entstehende ungleichmäßige Druckübertragung können die Längsfugen bei größerer Anzahl Segmente pro Ring nur etwa halb so stark zusammengedrückt werden wie bei einer geringeren Anzahl von Segmenten.

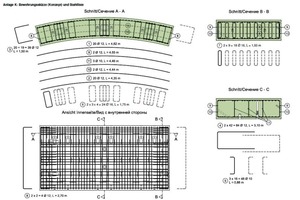
Bei großen Ringen wird die Ringteilung durch das maximale Transportgewicht mitbestimmt. Beim Orlovski-Tunnel mit einem Außendurchmesser von 18,65 m, einer Segmentdicke von 70 cm und einer Ringlänge von 2,20 m wiegt der Ring ca. 215 t. Da ein Lkw dort höchstens 18 t transportieren kann, musste eine Ringteilung von 12 Normalsegmenten plus ein kleiner Schlussstein gewählt werden (Bild 7).

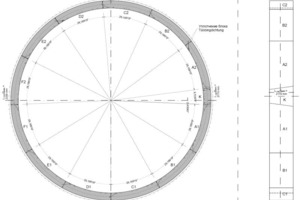
Obwohl der Tunnel annähernd gerade verläuft,

R_{min horizontal} = 5000 m,

R_{min vertikal} = 6000 m

wird der Ring konisch ausgeführt (Bild 8). Die Vortriebsmaschine fährt mit kleineren Kurven um die Solltunnelachse, realistisch ist eine Auffahrtoleranz von 10 cm. Der Tübbingring muss dieser Schildspur immer zwängungsfrei folgen können. Die schräge Ringseite muss auf der schildabgewandten Seite angeordnet werden, um mit dem neu zu bauenden Ring sofort eine Korrektur einleiten zu können. Der Orlovski-Ring wird als Uniring mit einer Konizität von 60 mm ausgeführt. Die minimale Ringlänge wird in der Schlusssteinachse angeordnet. Damit sind Kurvenradien von ca. 700 m aufzufahren.

Sowohl bei den Längs- als auch bei den Ringfugen hat sich die „glatte Fuge“ durchgesetzt. In den Ringfugen wurde aufgrund der weichen Böden zusätzlich eine Nocke-/Topf-Verbindung vorgesehen, die jedoch mit einer ausreichenden Toleranz von 11 mm versehen wurde (Bild 9). Auf ausdrücklichen Wunsch des Auftraggebers wird der Ring mit je einer Kompressionsfugendichtung innen und außen geplant.

Als Toleranzausgleich in den Ringfugen werden Zwischenlagen aus Hartfaserplättchen verwendet. Bei einigen internationalen Projekten wurde auf die Zwischenlagen verzichtet und Beton auf Beton gebaut. Die Erfahrungen aus diesen Projekten zeigen, dass bei Einhaltung einer hohen Fertigungsgenauigkeit und eines sehr sorgfältigen Ringbaues keine zusätzlichen Abplatzungen oder Risse im Tübbing auftreten.

Auf ausdrücklichen Wunsch des Bauherrn werden an der Ringinnenseite und -außenseite je ein Kompressionsfugenband vorgesehen. Diese doppelte Dichtungsebene wird selten vorgesehen. Ein außenliegendes Band ist im Allgemeinen ausreichend.

6 Statische Berechnungen und Bemessung

Der Tübbingring wird üblicherweise als gekoppelter Doppelring mit einem Stabzugrechenprogramm berechnet (Bild 10). Scheibenberechnungen können bisher nur am Einzelring durchgeführt werden, denn die Ringkopplung kann bisher bei den meisten Programmen nicht oder nur sehr aufwändig modelliert werden.

Um die Grenzwerte für die Berechnung zu erfassen wird auch ein biegesteifer Ring und ein Ring mit reduzierter Biegesteifigkeit nach Muir Wood berechnet:

I reduziertes Flächenmoment 2. Grades

= 0,01057 m⁴/m

I_s Flächenmoment 2. Grades der Kontaktfläche

= 0,00739 m⁴/m

I_n Flächenmoment 2. Grades des Volltübbings  

= 0,02858 m⁴/m

m Anzahl Segmente ohne kleinen Schlussstein 

= 12

Beim Orlovski-Ring reduziert sich die Biegesteifigkeit des Gelenkringes nach Muir Wood um 63 %. Die hiermit berechneten Biegemomente weichen von der „genauen“ Ringberechnung mit simulierten Drehfedern in den Längsfugen lediglich um ca. 15 % ab.

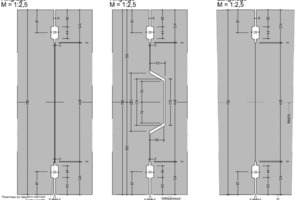
Bei großen Ringdurchmessern, mit rechnerisch größeren Verformungen, wird die Berechnung nach der Theorie 2. Ordnung erforderlich. Eventuell können Stabilitätsprobleme auftreten. In Bild 11 sind typische Schnittkraftverläufe für einen maßgeblichen Lastfall dargestellt.

Einen erheblichen Aufwand bereitet die Modellierung der Fugen und – nachfolgend - die dazugehörigen Detailnachweise:

• Nachweis der Teilflächenpressungen

• Nachweis der Spaltzugkräfte und Ermittlung der erforderlichen Bewehrung

Für Tübbingringe kann aufgrund von Versuchsergebnissen die zulässige Druckspannung in der Kraftübertragungszone auf die dreifache zulässige Betondruckspannung gesetzt werden (Tabelle 2).

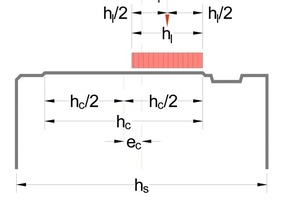
In der Berechnung wird die gedrückte Fugenfläche h_c um die doppelte Exzentrizität (Exzentrizität der Kontaktfläche e_c + Exzentrizität der Belastung e_l) reduziert:

h_l = h_c – 2 • (e_l + e_c)

Die Exzentrizität der Belastung ergibt aus den Schnittkräften:

Daraus wird die Druckspannung berechnet:

Die Spaltzugkräfte werden mit der größten Normalkraft und dem zugehörigen Biegemoment bzw. dem größten Biegemoment mit der zugehörigen Normalkraft berechnet.

F_Sd = 0,25 • N_d • (1 – h_l/h_s)

Die erforderliche Spaltzugbewehrung ergibt sich aus der Formel:

a_S = F_Sd/(f_yk • γ_S) [cm²/m]

Die Spaltzugspannungen und -kräfte in der Ringfuge werden üblicherweise mittels einer Scheibenberechnung am Einzeltübbing ermittelt (Bild 5). Die Spaltzugbewehrung kann daraus analog zur Spaltzugbewehrung in den Längsfugen berechnet werden. Am Ende der statischen Berechnungen und Nachweise werden die Bewehrungspläne konstruiert (Bild 13).

7 Stahlfaserbewehrte Tübbinge

Beton hat eine hohe Druckfestigkeit, jedoch nur eine geringe Zugfestigkeit, die zudem in den Berechnungen kaum angesetzt werden kann. Durch die Zugabe von Stahlfasern entsteht ein neuer homogener und isotroper Baustoff mit neuen Werkstoffkennwerten. Die Stahlfasern sind im Beton nicht richtungsorientiert, so dass Zugspannungen in allen Richtungen aufgenommen werden können (Bild 14). Zudem erhält der Beton eine hohe Duktilität. Die Gefahr von Abplatzungen und Rissen während des Transports, dem Einbau und dem Maschinenvorschub geht gegenüber herkömmlich bewehrten Tübbingen erheblich zurück.

Die Tübbinge können mit ausschließlicher Stahlfaserbewehrung, aber auch mit Stahlfasern in Kombination mit Stabbewehrung, produziert werden. Die verwendeten Stahlfasern sind üblicherweise 40 bis 60 mm lang, haben einen Durchmesser von ca. 1 mm und sind an den Enden zur Verankerung aufgebogen. Der Mindestfasergehalt sollte ca. 25 kg/m³ betragen, für die meisten Projekte wird ein Fasergehalt von 30 bis 50 kg/m³ verwendet. Sämtliche Nachweise müssen geführt werden, wobei insbesondere der Spaltzugnachweis häufig Probleme bereitet.

Stahlfaserbewehrte Tübbinge sind üblicherweise nur bei Ringen wirtschaftlich, die keine allzu großen Biegemomente und Teilflächenpressungen erhalten. Muss Stabbewehrung zur Aufnahme der Zugspannungen zugelegt werden, steigen die Produktionskosten sofort erheblich an. Die statischen Nachweise für faserbewehrte Ringe erfordert eine enge Zusammenarbeit zwischen Aufsteller, Prüfingenieur und Tunnelbausachverständigen. In Deutschland ist eine Zulassung im Einzelfall erforderlich.

Für den Orlovski-Tunnel wurde der Einsatz von Stahlfasertübbingen untersucht, für die hochbeanspruchten Tübbinge wäre jedoch ein hoher Anteil an zusätzlicher Stabbewehrung erforderlich gewesen. Somit wurde der Einsatz von Stahlfasern nicht weiter verfolgt.

8 Zusammenfassung

Das Tübbingdesign für große Ringdurchmesser verlangt eine enge und partnerschaftliche Zusammenarbeit zwischen allen Beteiligten. Die Baugrundkennwerte, Einwirkungen und Ringabmessungen müssen gemeinsam mit den Bauingenieuren, den Baugrundfachleuten, dem Maschinenhersteller und den Logistikfachleuten festgelegt werden. Während der Planungsphase muss das Ringkonzept laufend auf neue Erkenntnisse angepasst werden.

Wie bereits Sir Allen Muir Wood in seinem Buch „Civil Engineering in Context“ geschrieben hat:

„Das wichtigste Designelement ist deshalb, dass der Entwurf in ständigen Schleifen erfolgt, wobei jede Schleife eine Kommunikation zwischen Menschen oder zwischen Menschen und Computern beinhaltet.“

Am Beispiel Orlovski-Tunnel in St. Petersburg ist zu erkennen, dass Tunneldurchmesser, die noch vor wenigen Jahren für einen Maschinenvortrieb als nicht machbar galten, umgesetzt werden können. Dabei müssen, abgesehen von den maschinentechnischen Herausforderungen, neue Einwirkungsdimensionen auf den Tübbingring beherrscht und die Machbarkeit nachgewiesen werden.